sketch
//Anna Gusman
//agusman@andrew.cmu.edu
//Section E
//
//Project 06 Abstract Clock
var prevSec;
var millisRolloverTime;
var circleorigin = 0;
var milsecangle = 0;
var secondsangle = 0;
var minutesangle = 0;
var hoursangle = 0;
var degreespmsec;
var degreespsec;
var degreespmin;
var degreesphour;
//--------------------------
function setup() {
createCanvas(300, 300);
background(255);
millisRolloverTime = 0;
angleMode(DEGREES);
}
//--------------------------
function draw() {
background(255, 10);
// Fetch the current time
var H = hour();
var M = minute();
var S = second();
// Reckon the current millisecond,
// particularly if the second has rolled over.
// Note that this is more correct than using millis()%1000;
if (prevSec != S) {
millisRolloverTime = millis();
}
prevSec = S;
var mils = floor(millis() - millisRolloverTime);
var hourBarWidth = map(H, 0, 23, 0, width);
var minuteBarWidth = map(M, 0, 59, 0, width);
var secondBarWidth = map(S, 0, 59, 0, width);
// Make a bar which *smoothly* interpolates across 1 minute.
// We calculate a version that goes from 0...60,
// but with a fractional remainder:
var secondsWithFraction = S + (mils / 1000.0);
var secondsWithNoFraction = S;
var secondBarWidthChunky = map(secondsWithNoFraction, 0, 60, 0, width);
var secondBarWidthSmooth = map(secondsWithFraction, 0, 60, 0, width);
noFill();
// ellipse(150, 150, 135, 135);
// stroke(0, 10);
// ellipse(150, 150, hourBarWidth, hourBarWidth);
// stroke(0);
// ellipse(150, 150, secondBarWidthChunky, secondBarWidthChunky);
// stroke(0);
// ellipse(150, 150, secondBarWidthSmooth, secondBarWidthSmooth);
// stroke(0);
// ellipse(150, 150, minuteBarWidth, minuteBarWidth);
degreespmsec = map(S + (mils / 1000.0), 0, 59, 0, 360);
push();
translate(150, 150);
rotate(milsecangle);
stroke(255, 0, 0);
ellipse(30, 30, 50, 50);
pop();
milsecangle = degreespmsec;
degreespsec = map(S, 0, 59, 0, 360);
push();
translate(150, 150);
rotate(secondsangle);
stroke(255, 0, 0);
ellipse(30, 30, 50, 50);
ellipse(38, 38, 75, 75);
pop();
secondsangle = degreespsec;
degreespmin = map(M, 0, 59, 0, 360);
push();
translate(150, 150);
rotate(minutesangle);
stroke(0, 0, 255);
ellipse(95, 95, 30, 30);
pop();
minutesangle = degreespmin;
degreesphour = map(H, 0, 11, 0, 360);
push();
translate(150, 150);
rotate(hoursangle);
stroke(0, 255, 0);
ellipse(20, 20, 250, 250);
pop();
hoursangle = degreesphour;
// 30 * 12 = 360, different center for every hour, hoursangle
// then write mincircle function relative to that
//variable = 20, 0, + 30 degrees
}
//get center of outside circle
//
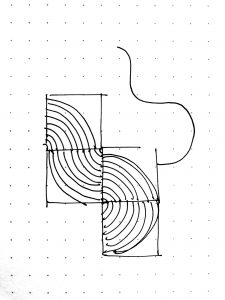
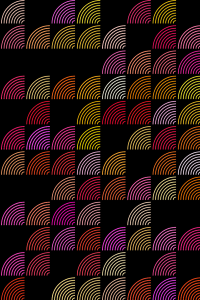
I think I am on the cusp of honing in on a very interesting interaction, but the final execution in the period of time we were allotted isn’t very satisfactory to me. I was inspired to create a clock based on an optical illusion of circular infinity- after coming across this captivating image, I entertained myself with trying to map out the logic behind it:

In my logic, I detail how the circles would be drawn from the outside in, and then rotating the circle matrix by the corresponding time (e.g. mapping 12 (hours) or 60 (seconds) to 360 (degrees)). I would then translate the matrix by the difference between the radius of the parent circle and the child circle. For some reason I’m unsure of, the content uploads folder won’t accept my jpegs or pngs of my sketch work, so I’ll try to amend that as soon as possible.
![[OLD FALL 2017] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)
















 ”
”
