Author: Christopher Reyes

creyes1-Project-07-Curves

creyes1 Project-07

//Christopher Reyes
//Section D
//creyes1@andrew.cmu.edu
//Project-07 (Composition with Curves)

var nPoints = 10000;

function setup() {
    createCanvas(480, 480);
    background(57, 64, 83);
}

function draw() {
    background(57, 64, 83);
    noStroke();

    //Darker circle
    fill(78, 74, 89);
    ellipse(width/2, height/2, 250, 250);

    //Lighter inner circle
    fill(110, 99, 98);
    ellipse(width/2, height/2, 200, 200);

    //Orbitals
    orbiter(0, 360, 200, 10);
    orbiter(0, 360, -200, 10);
    orbiter(360, 0, 175, 20);
    orbiter(360, 0, -175, 20);

    //Biggest, green rose
    push();
    translate(width/2, height/2);
    roseCurve(50, 200, 0, 10,
              [124, 174, 122],
              map(mouseY, 0, height, 1, 2.5));
    pop();

    //Medium rose
    push();
    translate(width/2, height/2);
    angleMode(DEGREES);
    rotate(180+45);
    angleMode(RADIANS);
    roseCurve(50, 180, 0, 10,
              [131, 144, 115],
              map(mouseY, 0, height, .5, 2));
    pop();

    //Smallest, white rose
    push();
    translate(width/2, height/2);
    angleMode(DEGREES);
    rotate(180-45);
    angleMode(RADIANS);
    roseCurve(0, 140, 0, 10,
              [255, 255, 255, 150],
              map(mouseY, 0, height, .1, .8));
    pop();

}

//Draws a rose curve where a and b values are determined by mouse position
function roseCurve(amin, amax, bmin, bmax, col, thickness) {
    var x;
    var y;
    var r;

    //Determines size of petals
    var a = map(mouseY, 0, height, amin, amax);
    //Determines number of petals
    var b = map(constrain(mouseX, 0, width), 0, width, bmin, bmax);

    noFill();
    stroke(col);
    strokeWeight(thickness);
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);

        r = a*sin(b*t);

        x = r * cos(t);
        y = r * sin(t);
        vertex(x, y);
    }
    endShape();
}

//Draws an ellipse that rotates around center according to mouse position
function orbiter(angleMin, angleMax, y, size) {
    push();
    translate(width/2, height/2);
    angleMode(DEGREES);
    rotate(map(mouseX, 0, width, angleMin, angleMax));
    noStroke();
    fill(110, 99, 98);
    ellipse(0, y, size);
    angleMode(RADIANS);
    pop();
}

I had forgotten how much I liked math and playing around with graphs, so I really enjoyed the time I spent with this project. Before I started my code, I explored and experimented a lot with Desmos, an online graphing calculator, and manipulated different variables of each equation to see what kind of movement I could get.

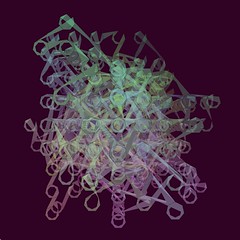
I ultimately went with the rose curve, a polar graph that’s visually interesting in not only its form, but in the way that the curve is drawn and generated. The main variables in the curve determine both the rose’s size and the amount of petals on it, so I decided to map both those variables to the mouse’s position and see what came out of it.

I’m definitely pleased with the final result, although I had initially wanted to make the orbitals travel in a sine wave around the circle, but it began to take a toll on the program’s ability to run smoothly, and ultimately settled on having it rotate without depending on a formula.

creyes1-LookingOutwards-07

Back in 2016, design firm CLEVER°FRANKE and fashion brand Byborre collaborated with Red Bull on their “RedBull Playrooms” event in order to track and visualize various datapoints in a club setting. Wearing bracelets designed by Byborre that monitored clubgoers’ movement, temperature, and excitement, visualizations of that data were generated using Processing and the Adobe Creative Suite in order to create both live animations that were projected on screens throughout the night, as well as a personalized printed “Flight of the Night,” which showed how a particular clubgoer spent their night – which rooms they frequented, which songs got them the most excited, and so on.

What I found interesting about this project was that clubgoers were receiving feedback as to how the night was going in real time, which is both interesting for the partygoer, and helpful in understanding what about an event is the most engaging and effective, allowing for better planning and overall better experiences. While it’s fun to see this in a recreational club setting, I’m curious to see what would come from applying the same technology and visualization practices to other settings, and if that data could be used to improve those spaces and experiences.

More work by CLEVER°FRANKE can be found on Behance or on their website.

creyes1-Project-06-Abstract-Clock

creyes1 Project-06 (Abstract Clock)

//Christopher Reyes
//Section D
//creyes1@andrew.cmu.edu
//Project-06 (Abstract Clock)

var prevSec;
var millisRolloverTime;

var moonX = 280;
var moonY = 160;
var moonSize = 260;
var moonShadowSize = moonSize*.9

var bgColor = [192, 214, 180];

var jewelHue;
var bgColorH;

var cx = moonX;
var cy = moonY;

function setup() {
    createCanvas(480, 480);
    colorMode(HSL);
    angleMode(DEGREES);
    background(bgColor);
    millisRolloverTime = 0;
}

function draw() {
    var H = hour();
    var M = minute();
    var S = second();

    if (prevSec != S) {
        millisRolloverTime = millis();
    }
    prevSec = S;
    var mils = floor(millis() - millisRolloverTime);

    var secondsWithFraction   = S + (mils / 1000.0);
    var secondsWithNoFraction = S;

    //Converts current time to a number between 0 and 24
    var currentTime = H + (M/60) + (secondsWithFraction/3600);

    //Changes background color every minute, lighter in AM, darker in PM
    var bgColorH = map(currentTime%6, 0, 6, 0, 360);
    var bgColorS = map(currentTime, 0, 24, 30, 60);
    var bgColorL = map(currentTime, 0, 24, 80, 20);

    background(bgColorH, bgColorS, bgColorL);

    //Lighter background ellipse towards bottom
    noStroke();
    fill(bgColorH, bgColorS-5, bgColorL+5);
    ellipse(width/2, height, 500, 315);

    //Moon
    fill(0, 0, 90, 1);
    ellipse(moonX, moonY, moonSize);

    fill(0, 100, 100, 1);
    ellipse(moonX, moonY, moonSize*.95);

    fill(0, 0, 90, 1);
    moonDetail(moonX, moonY);

    //Moves shadow throughout the day, creating an eclipse at noon
    var moonShadowX = map(currentTime, 0, 24,
                          moonX-(moonSize/2+moonShadowSize/2),
                          moonX+(moonSize/2+moonShadowSize/2));

    //Moon Shadow, changes color along with background
    fill(bgColorH, bgColorS, bgColorL, 1);
    ellipse(moonShadowX, moonY, moonShadowSize);

    //Clockwise spinnning ring based on current secondsWithFraction
    stroke(0, 100, 100, 1);
    noFill();
    strokeWeight(5);

    push();
    translate(moonX, moonY);
    rotate(map(secondsWithFraction, 0, 60, 0, 360));
    arc(0, 0, moonSize*1.75, moonSize*1.75, 10, 110);
    arc(0, 0, moonSize*1.75, moonSize*1.75, 130, 230);
    arc(0, 0, moonSize*1.75, moonSize*1.75, 250, 350);
    pop();

    //Counter-clockwise spinning ring, also based on current secondsWithFraction
    strokeWeight(2);

    push();
    translate(moonX, moonY);
    rotate(map(secondsWithFraction, 0, 60, 360, 0));
    arc(0, 0, moonSize*1.7, moonSize*1.7, 10, 110);
    arc(0, 0, moonSize*1.7, moonSize*1.7, 130, 230);
    arc(0, 0, moonSize*1.7, moonSize*1.7, 250, 350);
    pop();

    noStroke();

    //Creates clouds that float across the screen every minute
    var cloudX = map(secondsWithFraction, 0, 60, -100, width+140);

    fill(0, 0, 95, .8);
    cloud((cloudX-40)*1.05, 250+35, 1);
    cloud((cloudX-30)*.9, 250-20, 1);
    cloud(cloudX, 250, 1);
    cloud((cloudX+20)*.95, 250-30, 1);
    cloud((cloudX+30)*1.1, 250+30, 1);
    cloud(cloudX+50, 250-25, 1);

    //Jewel color is 180 degrees less the background's hue, including wraparound
    var jewelHue = bgColorH - 180;

    if (bgColorH < 180) {
        jewelHue = 360 - (180-bgColorH);
    } else {
        var jewelHue = bgColorH - 180;
    }

    //Static jewels
    jewel(115, 275, 1, jewelHue);
    jewel(160, 350, .6, jewelHue);
    jewel(65, 375, .8, jewelHue);

    //Rotates 3 jewels around moon in a clock-like fashion according to time
    var handOffset = 270; //Readjusts hands to start at 0 mark of the clock
    var handPlace = moonSize;

    //Second hand
    var handAngleS = map(secondsWithFraction, 0, 60,
                         handOffset, 360+handOffset);
    jewel(computeX(handPlace, handAngleS), computeY(handPlace, handAngleS),
          .2, jewelHue);

    //Minute hand
    var handAngleM = map(M+(secondsWithFraction/60), 0, 60,
                         handOffset, 360+handOffset);
    jewel(computeX(handPlace, handAngleM), computeY(handPlace, handAngleM),
          .2, jewelHue);

    //Hour hand
    var handAngleH = map(currentTime%12, 0, 12, handOffset, 360+handOffset);
    jewel(computeX(handPlace, handAngleH), computeY(handPlace, handAngleH),
          .2, jewelHue);

}

function cloud(x, y, SCALE) {
    quad(x, y+(20*SCALE), x+(40*SCALE), y, x, y-(20*SCALE), x-(40*SCALE), y);
}

function moonDetail(x, y) {
    var moonDetailX = [x+55, x-25, x+20, x, x+70, x+103, x-70, x-55];
    var moonDetailY = [y-15, y-45, y-78, y+30, y+30, y-10, y, y+55];
    var moonDetailScale = [1.8, 1.2, .65, .8, .9, .5, .5, .3];

    for (var i = 0; i < 8; i++) {
        push();
        translate(moonDetailX[i], moonDetailY[i]);
        rotate(45)
        cloud(0, 0, moonDetailScale[i]);
        pop();
    }
}

function jewel(x, y, SCALE, col) {

    //I || Base shape
    fill(col, 54, 71);
    quad(x+(35*SCALE), y+(10*SCALE),
         x, y-(83*SCALE),
         x-(35*SCALE), y+(10*SCALE),
         x, y+(83*SCALE));

    //II
    fill(col, 68, 80);
    triangle(x-(35*SCALE), y+(10*SCALE),
             x-(10*SCALE), y+(20*SCALE),
             x, y-(83*SCALE));
    //III
    fill(col, 75, 75);
    triangle(x-(35*SCALE), y+(10*SCALE),
             x-(10*SCALE), y+(20*SCALE),
             x, y+(83*SCALE));

    //IV
    fill(col, 46, 64);
    triangle(x+(35*SCALE), y+(10*SCALE),
             x-(10*SCALE), y+(20*SCALE),
             x, y+(83*SCALE));

}

//Computes the X position of a point on a circle according to given parameters
function computeX(handRadius, angle) {
return cx + handRadius*cos(angle);
}

//Computes the Y position of a point on a circle according to given parameters
function computeY(handRadius, angle) {
return cy + handRadius*sin(angle);
}

For this project I wanted to loosely base it off of the eclipse mechanic I included in my Dynamic Drawing assignment, but still create a unique stand-alone image.

The shadow of the moon displays the time on a 24-hour cycle, eclipsing at noon every day, and all the colors of the image change throughout the course of the day in hue, saturation, and lightness. A lot of my process regarding this project simply came from experimenting and adding layers of elements to see what was effective.

Through the creation of this, I enjoyed being able to play around with the timing of my elements and seeing the little interactions between them as their cycles played out.

creyes1-LookingOutwards-06

pDnPjQtDSnUpUWphDm0PKuFp1lip7Q5lENel4HImNG0WA2goAuCE1wYsYIbt50XF
JUbd7ju8FHmftFhy7c9EjpYZC95ksxJr0e4kZujC7tVQKcpJrGx9kEUmcllMLnWC_g012_3600x3600

Since 2016, Joseph Pollock has been creating procedurally generated artwork using his own program written in C++ and OpenGL. Each image is actually a captured frame of these programs, which continuously animate – from there he does a small amount of manual photo-editing and stitching to create the final image. What’s really fascinating about this is that most of the compositions are solely up to the random nature of the program, making every image unique and engaging. Granted, what we’re seeing is Pollack’s curation of what his program produces, but that doesn’t make the final result any less impressive. I am curious, however, to see more of Pollack’s process and the animations from which he gets his stills. Even as still images, they have a living quality to them – growth and decay all at once.

More of Pollack’s work can be found on Flickr and GitHub.

creyes1-Project-05-Wallpaper

creyes1 Project-05

//Christopher Reyes
//Section D
//creyes1@andrew.cmu.edu
//Project-05 (Wallpaper)

var paleyellow = [255, 252, 125];
var clovergreen = [127, 201, 108];
var lightBlue = [232, 242, 247];
var gray = [122, 122, 122];

var circleSize1 = 6;
var circleSize2 = 10;
var petalWidth = 19;
var petalHeight = 46;
var angle = 0;

var spacingx = 80;
var spacingy = 60;
var offset = 30;


function setup() {
    createCanvas(480, 480);
    background(256);
    angleMode(DEGREES);
    noStroke();

    //Light blue circles between main elements
    for (var x = 1; x <=7; x++) {
            for (var y = 1; y <= 9; y++) {
                fill(lightBlue);
                ellipse(x*spacingx-(70), y*spacingy-(60), 20);
            }
    }

    //Draws alternating clovers and flowers down several columns
    for (var x = 1; x <= 7; x++) {
        if (x%2 === 0) {
            for (var y = 1; y <= 8; y++) {
                if (y%2 === 0) {
                    drawFlower(x*spacingx -offset, y*spacingy -offset, .4);
                } else {
                    drawClover(x*spacingx -offset, y*spacingy -offset, .4);
                }
            }
        } else {
            for (var y = 1; y <= 8; y++) {
                if (y%2 === 0) {
                    drawClover(x*spacingx -offset, y*spacingy -offset, .4);
                } else {
                    drawFlower(x*spacingx -offset, y*spacingy -offset, .4);
                }
            }
        }
    }

    noLoop();

}

//Draws a flower at designated coordinates and at selected scale
function drawFlower(x, y, SCALE) {

    //Gray center circle
    fill(122);
    ellipse(x, y, circleSize2 * SCALE);

    //Draws 8 yellow petals rotated around a center point
    for(var i = 0; i < 8; i++) {
        fill(paleyellow);
        push();
        translate(x, y);
        rotate(angle);
        ellipse(0, -35 * SCALE, petalWidth * SCALE, petalHeight * SCALE);
        fill(122);

        //Draws accent circles at top and bottom of flower
        if (i === 0 || i === 4) {
            fill(gray);
            ellipse(0, (-30-petalHeight) * SCALE, circleSize1 * SCALE);
            ellipse(0, (-20-petalHeight) * SCALE, circleSize2 * SCALE);
        }

        //Small gray circles between petals (8)
        pop();
        push();
        translate(x, y);
        rotate(angle+22.5);
        fill(gray);
        ellipse(0, -45 * SCALE, circleSize1 * SCALE);
        pop();

        angle += 45;
    }

}

function drawClover(x, y, SCALE) {
    fill(clovergreen);

    //Middle Leaf
    beginShape();
        vertex(x, y+(38.5*SCALE));

        bezierVertex(x, y+(38.5*SCALE),
                     x+(38*SCALE), y-(52.5*SCALE),
                     x+(27*SCALE), y-(59.5*SCALE));

        bezierVertex(x+(16*SCALE), y-(66.5*SCALE),
                     x, y-(38.5*SCALE),
                     x, y-(38.5*SCALE));

        bezierVertex(x, y-(38.5*SCALE),
                     x-(16*SCALE), y-(66.5*SCALE),
                     x-(27*SCALE), y-(59.5*SCALE));

        bezierVertex(x-(27*SCALE), y-(59.5*SCALE),
                     x-(38*SCALE), y-(52.5*SCALE),
                     x, y+(38.5*SCALE));
    endShape();

    //Middle-Right Leaf
    beginShape();
        vertex(x+(5.4*SCALE), y+(38.5*SCALE));

        bezierVertex(x+(5.4*SCALE), y+(38.5*SCALE),
                     x+(70*SCALE), y+(3.5*SCALE),
                     x+(67*SCALE), y-(5.5*SCALE));

        bezierVertex(x+(65*SCALE), y-(15.5*SCALE),
                     x+(42*SCALE), y-(7.5*SCALE),
                     x+(42*SCALE), y-(7.5*SCALE));

        bezierVertex(x+(42*SCALE), y-(7.5*SCALE),
                     x+(47*SCALE), y-(31.5*SCALE),
                     x+(37*SCALE), y-(33.5*SCALE));

        bezierVertex(x+(28*SCALE), y-(34.5*SCALE),
                     x+(5.4*SCALE), y+(38.5*SCALE),
                     x+(5.4*SCALE), y+(38.5*SCALE));
        endShape();

    //Middle-Left Leaf
    beginShape();
        vertex(x-(5.4*SCALE), y+(38.5*SCALE));

        bezierVertex(x-(5.4*SCALE), y+(38.5*SCALE),
                     x-(70*SCALE), y+(3.5*SCALE),
                     x-(67*SCALE), y-(5.5*SCALE));

        bezierVertex(x-(65*SCALE), y-(15.5*SCALE),
                     x-(42*SCALE), y-(7.5*SCALE),
                     x-(42*SCALE), y-(7.5*SCALE));

        bezierVertex(x-(42*SCALE), y-(7.5*SCALE),
                     x-(47*SCALE), y-(31.5*SCALE),
                     x-(37*SCALE), y-(33.5*SCALE));

        bezierVertex(x-(28*SCALE), y-(34.5*SCALE),
                     x-(5.4*SCALE), y+(38.5*SCALE),
                     x-(5.4*SCALE), y+(38.5*SCALE));
    endShape();

    //Far-Right Leaf
    beginShape();
        vertex(x+(15*SCALE), y+(38.5*SCALE));

        bezierVertex(x+(15*SCALE), y+(38.5*SCALE),
                     x+(75*SCALE), y+(37.5*SCALE),
                     x+(77*SCALE), y+(32.5*SCALE));

        bezierVertex(x+(79*SCALE), y+(27.5*SCALE),
                     x+(60*SCALE), y+(26.5*SCALE),
                     x+(60*SCALE), y+(26.5*SCALE));

        bezierVertex(x+(60*SCALE), y+(26.5*SCALE),
                     x+(74*SCALE), y+(15.5*SCALE),
                     x+(69*SCALE), y+(12.5*SCALE));

        bezierVertex(x+(63*SCALE), y+(9.5*SCALE),
                     x+(15*SCALE), y+(38.5*SCALE),
                     x+(15*SCALE), y+(38.5*SCALE));
    endShape();

    //Far-Left Leaf
    beginShape();
        vertex(x-(15*SCALE), y+(38.5*SCALE));

        bezierVertex(x-(15*SCALE), y+(38.5*SCALE),
                     x-(75*SCALE), y+(37.5*SCALE),
                     x-(77*SCALE), y+(32.5*SCALE));

        bezierVertex(x-(79*SCALE), y+(27.5*SCALE),
                     x-(60*SCALE), y+(26.5*SCALE),
                     x-(60*SCALE), y+(26.5*SCALE));

        bezierVertex(x-(60*SCALE), y+(26.5*SCALE),
                     x-(74*SCALE), y+(15.5*SCALE),
                     x-(69*SCALE), y+(12.5*SCALE));

        bezierVertex(x-(63*SCALE), y+(9.5*SCALE),
                     x-(15*SCALE), y+(38.5*SCALE),
                     x-(15*SCALE), y+(38.5*SCALE));
    endShape();

    //Gray ellipsoidal accents
    fill(gray);
    ellipse(x+(23*SCALE), y+(38.5*SCALE), 40 * SCALE, 12 * SCALE);
    ellipse(x-(23*SCALE), y+(38.5*SCALE), 40 * SCALE, 12 * SCALE);

    ellipse(x, y+(50.5*SCALE), circleSize2 * SCALE);
    ellipse(x, y+(61.5*SCALE), circleSize1 * SCALE);

    ellipse(x, y-(53.5*SCALE), circleSize2 * SCALE);
    ellipse(x, y-(64.5*SCALE), circleSize1 * SCALE);
}

I definitely enjoyed putting this project together and playing around with different elements, which forced me to figure out how to draw more complex forms using p5.js. Before trying to code this right away, I made different possible mockups in Adobe Illustrator, then translated it into Javascript. As for the final result, I’m happy with how it came out – my initial sketches had even more accent dots than the final, but it wound up looking too busy and were therefore removed.

creyes1-LookingOutwards-05

Created in January 2017 by Sasha Vinogradova, Gods of Egypt is a print series that reimagines Egyptian gods as more contemporary characters. The figures themselves – Anubis, Hathor, and Horus, in order – are sculpted and rendered using Maxon Cinema 4D and Zbrush, then manipulated with photo editing software for the final print.

   

Anubis and Horus from Vinogradova’s “Gods of Egypt”

I’ve always been interested in mythology and ancient world religions, so to see them reimagined into something more modern while keeping the original context in mind is really admirable. Vinogradova achieves this with an incredible degree of photorealism that I initially thought this was straight photography and photomanipulation. It’s a really interesting and satisfying blend of mediums that Vinogradova includes here, with small graphical elements bringing out the quality of the sculpture.

This project along with Vinogradova’s other work can be found on both her website and Behance.

creyes1-Project-04-String-Art

creyes1 Project-04

//Christopher Reyes
//Section D
//creyes1@andrew.cmu.edu
//Project-04 (String Art)

//Variables for all 4 quadrants of diamond, counter-clockwise from top-right
var x1q1 = 200;
var y1q1 = 0;
var y1q1Interval = 5;
var x2q1 = 200;
var x2q1Interval = 5;
var y2q1 = 150;

var x1q2 = 200;
var y1q2 = 0;
var y1q2Interval = 5;
var x2q2 = 200;
var x2q2Interval = 5;
var y2q2 = 150;

var x1q3 = 200;
var y1q3 = 300;
var y1q3Interval = 5;
var x2q3 = 200;
var x2q3Interval = 5;
var y2q3 = 150;

var x1q4 = 200;
var y1q4 = 300;
var y1q4Interval = 5;
var x2q4 = 200;
var x2q4Interval = 5;
var y2q4 = 150;

//Variables for counter-clockwise spinning blue ring
var angleRing1 = 0;
var innercircleSaturation = 74;
var saturationInterval = -1;

//Variables for clockwise spinning rainbow ring
var angleRing2 = 0;
var circleHue = 0;

//Centerpoint to base rings off of
var cx = 200; //X coordinate of circle origin
var cy = 150; //Y coordinate of circle origin

function setup() {
    createCanvas(400, 300);
    background(229, 225, 174); //Darker yellow background
    angleMode(DEGREES);

    noStroke();

    fill(252, 248, 194); //Lighter yellow circle
    ellipse(width/2, height/2, 350, 350);

    fill(158, 224, 239); //Sky blue circle
    ellipse(width/2, height/2, 245, 245);

    fill(256, 40); //Transparent white circles
    ellipse(100, 100, 300, 300);
    ellipse(300, 200, 300, 300);
    ellipse(300, 100, 300, 300);
    ellipse(100, 200, 300, 300);

    //Diamond, Quadrant 1
    for(var i = 1; i <= 40; i++) {
        x2q1 += x2q1Interval;
        y1q1 += y1q1Interval;
        stroke(256);
        line(x1q1, constrain(y1q1, 30, 150), constrain(x2q1, 200, 320), y2q1);
    }

    //Diamond, Quadrant 2
    for (var i = 1; i <= 40; i++) {
        x2q2 -= x2q2Interval;
        y1q2 += y1q1Interval;
        stroke(230);
        line(x1q2, constrain(y1q2, 30, 150), constrain(x2q2, 80, 200), y2q2);
    }

    //Diamond, Quadrant 3
    for (var i = 1; i <= 40; i++) {
        x2q3 -= x2q3Interval;
        y1q3 -= y1q3Interval;
        stroke(256);
        line(x1q3, constrain(y1q3, 150, 270), constrain(x2q3, 80, 200), y2q3);
    }

    //Diamond, Quadrant 4
    for (var i = 1; i <= 40; i++) {
        x2q4 += x2q4Interval;
        y1q4 -= y1q4Interval;
        stroke(230);
        line(x1q4, constrain(y1q4, 150, 270), constrain(x2q4, 200, 320), y2q4);
    }

}

function draw() {

    colorMode(HSB);

    //Creates a constantly-looping, counter-clockwise spinning
    //blue ring with a varying saturation
    for(var i = 1; i <=1; i++) {
        angleRing1 -= 5
        stroke(205, innercircleSaturation, 105);
        line(computeX(50, angleRing1), computeY(50, angleRing1),
            computeX(50, angleRing1+140), computeY(50, angleRing1+140));
        innercircleSaturation += saturationInterval;
        //Switches b/w increasing & decreasing saturation at certain thresholds
        if (innercircleSaturation < 20 && saturationInterval < 0 ||
            innercircleSaturation > 74 && saturationInterval > 0) {
            saturationInterval = -saturationInterval;
        }
    }

    //Creates a constantly-looping, clockwise spinning rainbow ring
    for(var i = 1; i <=1; i++) {
        angleRing2 += 5
        stroke(circleHue, 52, 70);
        line(computeX(350, angleRing2), computeY(350, angleRing2),
             computeX(350, angleRing2+140), computeY(350, angleRing2+140));
        circleHue += 15;
        //Resets hue of line drawn to H = 0 to make a continuous transition
        if (circleHue > 360) {
            circleHue = 0;
        }
    }

}

//Computes the X position of a point on a circle according to given parameters
function computeX(ringRadius, angle) {
    return cx + ringRadius*cos(angle);
}

//Computes the Y position of a point on a circle according to given parameters
function computeY(ringRadius, angle) {
    return cy + ringRadius*sin(angle);
}

I was initially unsure as to how to approach this project, but I was somewhat inspired by circular string art patterns and – after accidentally creating several infinite loops while figuring out this week’s assignments – the motion of loading cursors (the blue ring on Windows and rainbow pinwheel on iOS). I’m definitely pleased with the final product, and enjoyed being able to experiment with parameters and seeing the various effects it could have on the program. For instance, the rainbow swirl was initially an accident, but it forced me to look into precisely what that code was doing, understanding it, and then modifying and leveraging it in order to achieve the final effect.

creyes1-LookingOutwards-04


A promotional video for On Your Wavelength & Merge Festival 2015

Created by Marcus Lyall, Robert Thomas, and Alex Anpilogov, On Your Wavelength is an interactive installation that generates music and a laser-show as it analyzes the user’s brainwaves in real-time.

In the installation, the user is equipped with EEG brain scanner headseat, which is then analyzed turned into media using Processing and Pure Data for audio generation. The analysis creates a profile of the user and focuses on three possible emotions – joy, detachment, and tension – along with several possible instruments and pitches in order to generate musical compositions specific to the current user. While the generation was up to the program’s analysis, the color choices and compositions, as well as the distinctive emotions that they chose to go by show the distinct mark of the artists who worked on it.


Behind the scenes of On Your Wavelength

Large-scale, immersive experiences like this one have always been fascinating to me, and in this case it’s not just technology taking artistic control, but rather a symbiotic relationship between user and program that’s not only awe-inspiring to look at, but especially to be in the user’s place and see how the program reacts.

On Your Wavelength was first shown during Merge Festival 2015 in London and later in a modified format in Winter Lights 2017 in London.

Additional performances, such as this one, can be viewed on Youtube.


“Lime,” an On Your Wavelength performance

creyes1-Project-03-Dynamic-Drawing

creyes1-Project-03 Dynamic Drawing

//Christopher Reyes
//Section D
//creyes1@andrew.cmu.edu
//Project-03 (Dynamic Drawing)

var backgroundR = 209
var backgroundG = 153
var backgroundB = 198

var ringSize = 0
var ringColor= 256

function setup() {

    createCanvas(640, 480);
    angleMode(DEGREES);

}

function draw() {

    var colorConstrain = constrain(mouseX, 102, 540)

    background(backgroundR, backgroundG, backgroundB);
    fromBG = color(209, 153, 198);
    toBG = color(199, 211, 183);
    backgroundColor = lerpColor(fromBG, toBG, mouseX/width);
    background(backgroundColor);

    var moonConstrainX = constrain(mouseX, 102, 540)

    //Moon, moves in the X direction as mouseX changes
    noStroke();
    fill(256);
    ellipse(moonConstrainX, 80, 64, 64);

    //Moon shadow, follows moon at a rate that eventually overtakes it
    //Color set to be the same as the background to hide it
    fill(backgroundR, backgroundG, backgroundB);
    fill(backgroundColor);
    ellipse(moonConstrainX*1.30 - 95, 80, 54, 54);

    //Mountain ring, changes scale according to mouseX
    noFill();
    stroke(ringColor);
    strokeWeight(5);
    ringSize = constrain(mouseX, 100, 545) - 100
    ellipse(248, 158, ringSize, ringSize);

    //Secondary rings that rotate while revolving around mountain's peak,
    //based on mouseX position
    var spinConstraint = constrain(mouseX, 102, 540)

    push();
    translate(248, 158);
    rotate(spinConstraint);
    arc(248, 158, ringSize, ringSize,
        spinConstraint + 5, spinConstraint + 115);
    arc(248, 158, ringSize, ringSize,
        spinConstraint + 125, spinConstraint + 235);
    arc(248, 158, ringSize, ringSize,
        spinConstraint + 245, spinConstraint + 355);
    pop();

    push();
    translate(248, 158);
    rotate(spinConstraint - 160);
    arc(248, 158, ringSize*.75, ringSize*.75,
        spinConstraint + 5, spinConstraint + 115);
    arc(248, 158, ringSize*.75, ringSize*.75,
        spinConstraint + 125, spinConstraint + 235);
    arc(248, 158, ringSize*.75, ringSize*.75,
        spinConstraint + 245, spinConstraint + 355);
    pop();

    //Hides rings when they get too small - given same color as background
    if (ringSize == 0) {
        ringColor = backgroundColor;
    } else {
        ringColor = 256;
    }

    noStroke();

    //Draws triangles for mountains that change colors as mouseX changes
    //Note: For organization, for each mountain, the left side is drawn first
    //
    //Mountain color variable format: Mount(#)[(L)eft||(R)ight]

    //Mountain 1, transitions from pink to blue
    fill(232, 151, 168);
    fromMount1L = color(232, 151, 168);
    toMount1L = color(105, 175, 173);
    mount1LColor = lerpColor(fromMount1L, toMount1L, mouseX/width);
    fill(mount1LColor);
    triangle(111, 226, 57, 416, -3, 416);

    fill(206, 122, 137);
    fromMount1R = color(206, 122, 137);
    toMount1R = color(97, 142, 153);
    mount1RColor = lerpColor(fromMount1R, toMount1R, mouseX/width);
    fill(mount1RColor);
    triangle(111, 226, 57, 416, 189, 416);

    //Mountain 2, pink
    fill(232, 151, 168);
    triangle(41, 254, -13, 444, -73, 444);
    fill(206, 122, 137);
    triangle(41, 254, -13, 444, 119, 444);

    //Mountain 3, pink
    fill(232, 151, 168);
    triangle(510, 366, 456, 556, 396, 556);
    fill(206, 122, 137);
    triangle(510, 366, 456, 556, 588, 556);

    //Mountain 4, largest, transitions from yellow to navy
    fill(229, 225, 163);
    fromMount4L = color(229, 225, 163);
    toMount4L = color(31, 60, 78);
    mount4LColor = lerpColor(fromMount4L, toMount4L, mouseX/width);
    fill(mount4LColor);
    triangle(248, 158, 154, 480, -111, 480);

    fill(214, 192, 123);
    fromMount4R = color(214, 192, 123);
    toMount4R = color(10, 30, 49);
    mount4RColor = lerpColor(fromMount4R, toMount4R, mouseX/width);
    fill(mount4RColor);
    triangle(248, 158, 154, 480, 591, 480);

    //Stray cloud with transparency
    fill(256, 125);
    quad(210.5, 272, 250.5, 290, 210.5, 308, 170.5, 290);

    //Mountain 5, transitions from pink to dark green
    fill(232, 151, 168);
    fromMount5L = color(232, 151, 168);
    toMount5L = color(51, 93, 97);
    mount5LColor = lerpColor(fromMount5L, toMount5L, mouseX/width);
    fill(mount5LColor);
    triangle(193, 290, 139, 480, 79, 480);

    fill(206, 122, 137);
    fromMount5R = color(206, 122, 137);
    toMount5R = color(37, 77, 68);
    mount5RColor = lerpColor(fromMount5R, toMount5R, mouseX/width);
    fill(mount5RColor);
    triangle(193, 290, 139, 480, 271, 480);

    //Mountain 6, transitions from blue to pale green
    fill(175, 232, 229);
    fromMount6L = color(175, 232, 229);
    toMount6L = color(170, 191, 156);
    mount6LColor = lerpColor(fromMount6L, toMount6L, mouseX/width);
    fill(mount6LColor);
    triangle(108, 334, 93, 480, -30, 480);

    fill(127, 201, 201);
    fromMount6R = color(127, 201, 201);
    toMount6R = color(130, 171, 142);
    mount6RColor = lerpColor(fromMount6R, toMount6R, mouseX/width);
    fill(mount6RColor);
    triangle(108, 334, 93, 480, 253, 480);

    //Mountain 7, transitions from green to light blue
    fill(160, 232, 160);
    fromMount7L = color(160, 232, 160);
    toMount7L = color(105, 175, 173);
    mount7LColor = lerpColor(fromMount7L, toMount7L, mouseX/width);
    fill(mount7LColor);
    triangle(295, 323, 229, 480, 153, 480);

    fill(117, 175, 117);
    fromMount7R = color(117, 175, 117);
    toMount7R = color(97, 142, 153);
    mount7RColor = lerpColor(fromMount7R, toMount7R, mouseX/width);
    fill(mount7RColor);
    triangle(295, 323, 229, 480, 399, 480);

    //Clouds with transparency
    fill(256, 125);
    quad(332.5, 231, 372.5, 249, 332.5, 267, 292.5, 249);
    quad(393.5, 217, 433.5, 235, 393.5, 253, 353.5, 235);
    quad(298.5, 240, 338.5, 258, 298.5, 276, 258.5, 258);
    quad(275.5, 235, 315.5, 253, 275.5, 271, 235.5, 253);
    quad(258.5, 214, 298.5, 232, 258.5, 250, 218.5, 232);
    quad(313.5, 265, 353.5, 283, 313.5, 301, 273.5, 283);
    quad(339.5, 369, 379.5, 387, 339.5, 405, 299.5, 387);
    quad(403.5, 258, 443.5, 276, 403.5, 294, 363.5, 276);
    quad(353.5, 265, 393.5, 283, 353.5, 301, 313.5, 283);

}

Admittedly, it took me a while to come to this final idea, as a lot of my ideas required code that was out of my current technical abilities, although I do hope to act on them sometime in the future. After mocking up a design in Illustrator, I wanted to have a drawing that transitioned between states rather than an open-ended series of relations. I had some difficulties figuring out exactly how to execute all of the color transitions, but lerpColor(); wound up being the perfect solution, where the color in between the two I specified was determined by the mouse’s X position relative to the width of the canvas, creating the required interval number between 0-1. After finally figuring that out, the rest was a lot of trial and error, playing around with the code in order to see what kind of movement could be created while still making sense composition-wise.

creyes1-LookingOutwards-03

Mohanned Iskanderani’s RAYGON

Created in 2016 by Mohanned Iskanderani, the RAYGON lamp is created solely from the parametric graphic algorithm editor, Grasshopper, so that as Iskanderani describes, “the computer is allowed to design as much as the designer is.”

What’s really astounding about this project is that while the script was created by hand, the actual form of the lamp was entirely computer-generated, and likely easily modifiable. With this, it allows further experimentation of customized intricate designs that would otherwise be difficult to manually create. Of course, Iskanderani still had a hand in creating the final lamp form, with his main goal being to create a lamp that projected a unique pattern to truly fill the space in which it resides. The final product is something that makes itself known not simply to make itself the focal point, but to enhance the room that surrounds it.

RAYGON is still under development, and not much information regarding it has been made available since its initial appearance, but is intended to be 3D printed in plastic and finished in some other material.

RAYGON earned an Honorable Mention in the 2016 VMODERN Furniture Design Competition. The project is also available to view on Behance.