/*Jessica Nip
Section A
jknip@andrew.cmu.edu
Project-07
*/
//-------------------------
function setup() {
createCanvas(480,480);
}
//-------------------------
function draw() {
background(80);
//draw hypotrochoid curve
//define parametric variables, map and constrain mouseX and Y
var h = map(mouseY, 0, height/4, height/2, height/4);
var a = constrain(mouseX, 0, width/4);
var b = 5;
//set visual variables
stroke(255,165,175);
fill(255,165,175);
//set up for loop to consider all 360 degrees
for (var t = 0; t < 360; t++) {
//convert parametric equation of curve
var x = width/2 +((a-b)*cos(radians(t)))+h*cos(((a-b)/b)*(radians(t)));
var y = height/2 + ((a-b)*sin(radians(t)))-h*sin(((a-b)/b)*(radians(t)));
//create tiny ellipses that repeat parametrically and create interactive collage
ellipse(x, y, 1, 1);
}
}




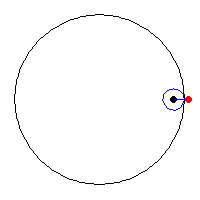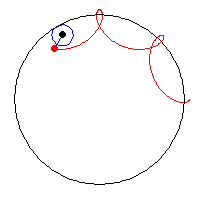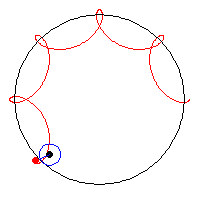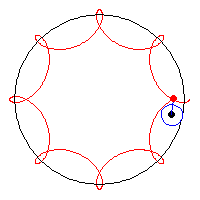
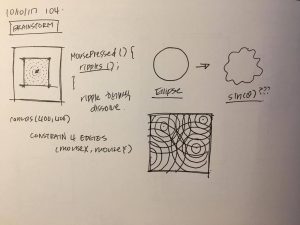
Inspired by the hypotrochoid, I enjoyed looking at its ‘drawing’ mechanism that considers a smaller circle rolling around the inside of a bigger circle and the form of curves it draws. I wanted to recreate it through fireworks-inspired specks, that form both typical geometric forms (e.g. circle) and its exploded perspectives — I also wanted this relationship to be mapped with the movement of mouseX and mouseY, which I have mapped and constrained to smaller sections of the canvas. The aesthetics of the project was also inspired by this minimalist ‘flicker’ of the supposedly ‘specks’ of the form, so I used two colors that drew a distinct contrast.
![[OLD FALL 2017] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)