//
// Supawat Vitoorapakorn
// Svitoora@andrew.cmu.edu
// Section E
//
// Squircle
// Equation from:
// https://en.wikipedia.org/wiki/Superellipse
w = 480;
h = 480;
//Signum function
function sgn(x) {
if (x > 0) {
return 1
}
if (x == 0) {
return 0
}
if (x < 1) {
return -1
}
}
//------------------------
var SQUIRCLE = []; // Array for nodes
var theta;
var a = w * .33 // Squircle width
var b = h * .33 // Squircle height
var n = 3.5 // roundness
// Create nodes for squircle
function create_squircle(x, y) {
this.x = x;
this.y = y;
}
// Calculate Squircle's X position from theta
function squircle_x() {
angleMode(DEGREES);
return abs(cos(theta)) ** (2 / n) * a * sgn(cos(theta))
}
// Calculate Squircle's Y position rom theta
function squircle_y() {
angleMode(DEGREES);
return abs(sin(theta)) ** (2 / n) * b * sgn(sin(theta))
}
// Create Squircle based on an interval of theta
// and push its node into an array
function make_squircle() {
angleMode(DEGREES);
//Plot every interval degree of squircle
interval = 1;
for (theta = 0; theta < 360; theta += interval) {
x = squircle_x(theta);
y = squircle_y(theta);
SQUIRCLE.push(new create_squircle(x, y))
}
}
var gon = 60;
var min_gon = 45;
var max_gon = 160;
var SWITCH = 1;
// Create a bounce loop animation from drawing lines
function gon_loop() {
print(SQUIRCLE.length)
if (gon == max_gon) {
SWITCH = -1;
print("inversing");
};
if (gon == min_gon) {
SWITCH = 1;
}
gon += SWITCH;
}
// Draws Squircle from array
function draw_squircle() {
//Draw Shape
if (inverse == 1) {
fill(255);
} else {
fill(0);
}
beginShape();
strokeWeight(1);
for (i in SQUIRCLE) {
x = SQUIRCLE[i].x
y = SQUIRCLE[i].y
curveVertex(x, y);
}
//Force Close Shape
curveVertex(SQUIRCLE[5].x, SQUIRCLE[5].y);
endShape(CLOSE);
connect_lines();
}
// Connect a point in squircle to every point
function connect_lines() {
//Add lines
if (inverse == 1) {
stroke(0, 0, 0, 255 * .1);
} else {
stroke(255, 255, 255, 255 * .1)
}
for (i in SQUIRCLE) {
x_0 = SQUIRCLE[i].x
y_0 = SQUIRCLE[i].y
for (i in SQUIRCLE) {
if (i % (gon) == 0) {
// %gon used to skip certains nodes
// to not overload the computer
x_1 = SQUIRCLE[i].x
y_1 = SQUIRCLE[i].y
line(x_0, y_0, x_1, y_1);
}
}
}
}
//------------------------
function setup() {
createCanvas(w, h);
background(255 * .75);
make_squircle();
print(SQUIRCLE.length / 2, SQUIRCLE.length / 6)
}
//------------------------
// Use mouseX to control the roundeness of squircle
function control_roundness() {
mousePos = (abs(mouseX - (w / 2)) / (w / 2));
mousePos = constrain(mousePos, 0, 1);
roundness = map(mousePos, 0, 1, .2, 10);
n = roundness;
SQUIRCLE.length = 0;
make_squircle();
}
//Use mouseY to control size of squircle
function control_size() {
mousePos = (abs(mouseY - (h / 2)) / (h / 2));
mousePos = constrain(mousePos, 0, 1);
size = map(mousePos, 0, 1.2, .175, .35);
a = w * size;
b = h * size;
SQUIRCLE.length = 0;
make_squircle();
}
function mouseClicked() {
inverse = inverse * -1;
}
//------------------------
var inverse = 1; // incerts color
function draw() {
if (inverse == 1) {
background(255 * .8);
} else {
background(255 * .1)
}
control_roundness();
control_size();
gon_loop(); //bounce animation for connecting line
//Draw Closed Shape
push()
translate((w / 2), (h / 2)) // center drawing
draw_squircle();
pop()
}Squircle
For my equation, I picked the superellipse equation which is capable of creating a squircle. I stumbled upon this equation on MathWorld:
Since this equation is not particularly helpful, I went on Wikipedia and found the parametric equation for the superellipse:
At first, I was a bit confused about what the signum sgn() function is, but after some googling, I understood it and was able to replicate the function easily in javascript. Initially, I thought about doing a spirograph whereby a pen would rotate around the moving point and generate a drawing with variable orbital roundness:
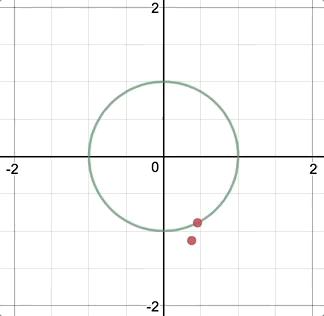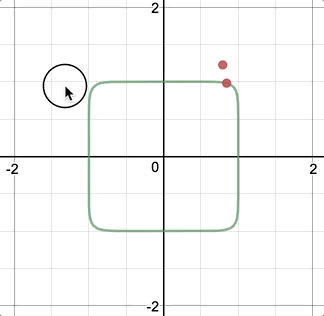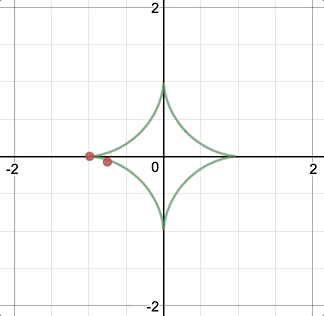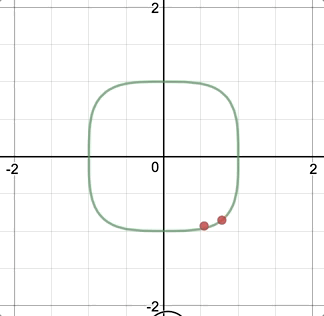
Variable Density
After re-building my equation in javascript, I found that the curve was denser in some area than others. This I believe is caused by the way that I parametrically constructed this curve via iterating from 0 to 360˚ and pushing the nodes into an array:
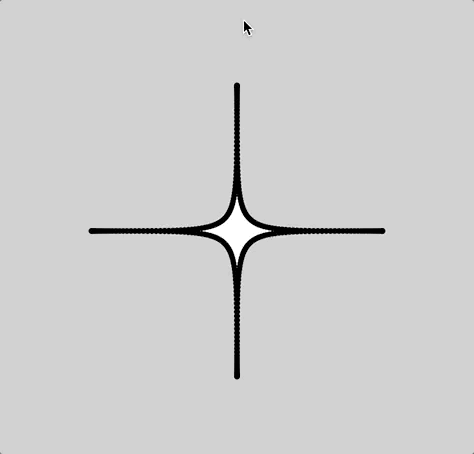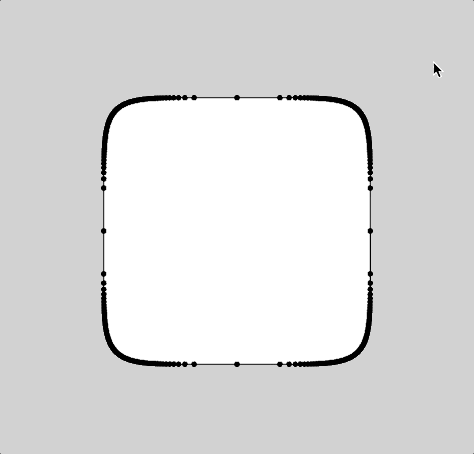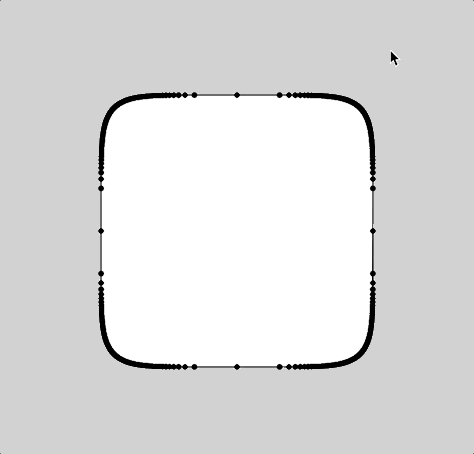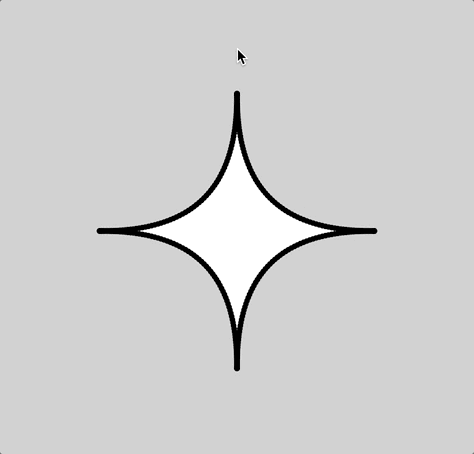
Had this been constructed through Calculus, these variable densities wouldn’t occur. But since these variable densities existed, I decided to take advantage of it use it as nodes to do a string art. These are the results:




![[OLD FALL 2017] 15-104 • Introduction to Computing for Creative Practice](wp-content/uploads/2020/08/stop-banner.png)

