//JooHee Kim
//Section E
//jooheek@andrew.cmu.edu
//Project-07
//This project is based on the epicycloid formula
//http://mathworld.wolfram.com/Epicycloid.html
function setup() {
createCanvas(480, 480);
angleMode(DEGREES);
}
function draw() {
background(0,30);
//moves lines to the middle of canvas
translate(width/2, height/2);
//draws 5 curve shapes in different sizes
for (var curveSize = 0; curveSize < 10; curveSize += 2) {
//draws lines on every angle of the curve in degrees mode
for (var i=0; i<360; i++) {
//variable that remaps mouseX from 0 to 12
//represents "a" in original formula
var M = map(mouseX, 0, width, 0, 12);
//represents "b" in original formula
var b = 5;
//variables of line coordinates drawn according to the epicycloid curve formula
//substitutes with M so that the size and number of petals change according to mouseX
var lineX1 = curveSize*((M+b)*cos(i-100) - b*cos(((M+b)/b)*i-100));
var lineY1 = curveSize*((M+b)*sin(i-100) - b*sin(((M+b)/b)*i-100));
var lineX2 = curveSize*((M+b)*cos(i) - b*cos(((M+b)/b)*i));
var lineY2 = curveSize*((M+b)*sin(i) - b*sin(((M+b)/b)*i));
//draw line with variables
stroke(i, 210, 210, curveSize);
line(lineX1, lineY1, lineX2, lineY2);
}
}
}
After looking at the types of curves that were given to us, I decided to choose the epicycloid. It uses a parametric equation:
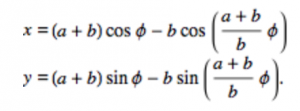
I first tried to figure out how the graph works in coding, and after trying out many options I liked using lines with graph formula. Although I thought this project was simpler than other projects, I found it fun using curve formulas to represent curves in different ways. I first started out with one curve shape but found that putting it in a for loop that varies in sizes makes it more interesting. I also had fun playing with the opacity in both the background and lines.

*There are more curves when looked on the browser than when looked in this WordPress blog.
![[OLD FALL 2017] 15-104 • Introduction to Computing for Creative Practice](wp-content/uploads/2020/08/stop-banner.png)