Month: October 2018

jenny’s sketch

//Jenny Hu
//Section E
//jjh1@andrew.cmu.edu
//Project 07


var nPoints = 250;


function setup() {
    createCanvas(450, 450);
  }


function draw() {
    background(250);
    
    // draw the curve
    push();
    translate(width / 2, height / 2);
    HypotrochoidCurves();
    pop();
}


///////


function HypotrochoidCurves() {

    var x;
    var y;
    var a = 90.0;
    var a2 = 30.0;

    var b = a / 2.0;
    var b2 = a2 / 10;
    var b3 = a / 15;

    var h1 = constrain(mouseY/2, 0, width/5);
    var h2 = constrain(mouseY/8, 0, width/2);
    var h3 = constrain(mouseX/5, 0, width/5);
    var h4 = constrain(mouseX/15, 0, width/10);

    var ph1 = mouseX / 50.0;
    var ph2 = mouseY / 25.0;


    // Hypotrochoid Curve 1 (light purple)
    fill(210, 200, 250);
    stroke(255);
    strokeWeight(2);

    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        
        x = (a2 + b3) * cos(t) + h1 * cos(ph2 + t * (a2 + b3) / b3);
        y = (a2 + b3) * sin(t) - h1 * sin(ph2 + t * (a2 + b3) / b3);
        vertex(x, y);
    }
    endShape(CLOSE);


    // Hypotrochoid Curve 2 (Pink)
    fill(255, 200, 200);
    stroke(255);
    strokeWeight(2);

    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        
        x = (a + b) * cos(t) + h2 * cos(ph1 + t * (a + b) / b);
        y = (a + b) * sin(t) - h2 * sin(ph1 + t * (a + b) / b);
        vertex(x, y);
    }
    endShape(CLOSE);

    // Hypotrochoid Curve 3 (Purple)
    fill(100, 110, 200);
    stroke(255);
    strokeWeight(2);
    beginShape();

    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        
        x = (a + b) * cos(t) + h3 * cos(ph2 + t * (a + b) / b);
        y = (a + b) * sin(t) - h3 * sin(ph2 + t * (a + b) / b);
        vertex(x, y);
    }
    endShape(CLOSE);

    // Hypotrochoid Curve 4 (green)
    fill(50, 210, 200);
    stroke(255);
    strokeWeight(2);
    beginShape();

    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        
        x = (a2 + b2) * cos(t) + h4 * cos(ph2 + t * (a2 + b2) / b2);
        y = (a2 + b2) * sin(t) - h4 * sin(ph2 + t * (a2 + b2) / b2);
        vertex(x, y);
    }
    endShape(CLOSE);
    
}

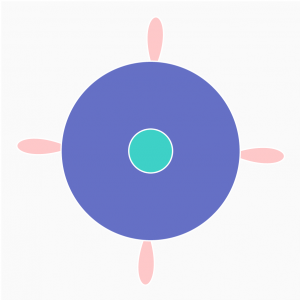
For this project, I created a layered set of different Hypotrochoids.  These parametric forms are altered differently and independently based on mouseX and mouseY. I found the Epitrochoid example from the blog really inspiring for its globby, blobby shape and movement and wanted to do the same for a roulette-like shape.

Please see the different shots below!

sketch
(Drag mouse to the pink circle to return to “butterfly” shape!)

/*
Eliza Pratt
Section E
elpratt@andrew.cmu.edu
Project 07
*/

//butterfly curve 
//http://mathworld.wolfram.com/ButterflyCurve.html

var mX; 
var mY;
var dis;
var wing = 4;
var size;
var col = 255;

function setup() {
    createCanvas(480, 480);

}

function draw() {
    background(0);
    stroke("deeppink");

    //draws pink circle
    ellipse(width/2, height/2, width/2, height/2);

    textFont("futura");
    textAlign(CENTER);
    textSize(18);
    text("Click and Drag", width/2, 430);

    //constrains mouse position to canvas size
    mX = constrain(mouseX, 0, width);
    mY = constrain(mouseY, 0, height);

    //measures distance between curve center and mouse position
    dis = dist(mX, mY, width/2, height/2);

    //assigns distance to correspond with curve amplitude
    size = map(dis, 0, width/2, 0, 50);

    //draws butterflys
    butterfly(wing/2, size/2, col/4);
    butterfly(wing - 1, 0.75 * size, col/2);
    butterfly(wing, size, col);



}

//draws butterfly with parameters to change 
//frequency, amplitude, and color
function butterfly(b, a, c) { 
    var x;
    var y;
    stroke(c);
    var points = 400; //number of points on curve
    noFill();

    beginShape();
    //calculates many x and y coordinates using curve function
    //plots vertices at coordinate points 
    for (var i = 0; i < points; i++) {
        var t = map(i, 0, points, 0, TWO_PI);

        //written notation: x = sin(t)[e^cos(t) - 2cos(4t) + sin^5 (t/12)]
        x = width/2 + sin(t) *  a * (Math.pow(Math.E, cos(t)) - 2 * cos(b * t) + Math.pow(sin(t/12), 5));
        y = height/2 + cos(t) * -a * (Math.pow(Math.E, cos(t)) - 2 * cos(b * t) + Math.pow(sin(t/12), 5));

        vertex(x, y);
    }
    endShape(CLOSE);

}

function mouseDragged() {
    //changes frequency of function based on mouse position
    wing = map(dis, 0, width/2, 2, 6);
}

Looking through all these curve functions has made me realize how much math I’ve forgotten in the past year! Nevertheless, I wanted to play around with some of the more complex curves from the website. I saw some pretty cool spirals with integrals but I couldn’t figure out the notation for javascript. The curve I made here is called a “butterfly curve”, but I overlapped a few of them with altered frequencies to explore some of the other cool shapes this function can produce. Drag your mouse around the canvas to check out the other curves! Dragging the mouse to any point on the circle will return it to a butterfly shape.