Responses to this prompt will be discussed in class on Wednesday, October 6. This set of prompts has two parts:
- Readings on Pattern
- A Tiling Pattern Composition
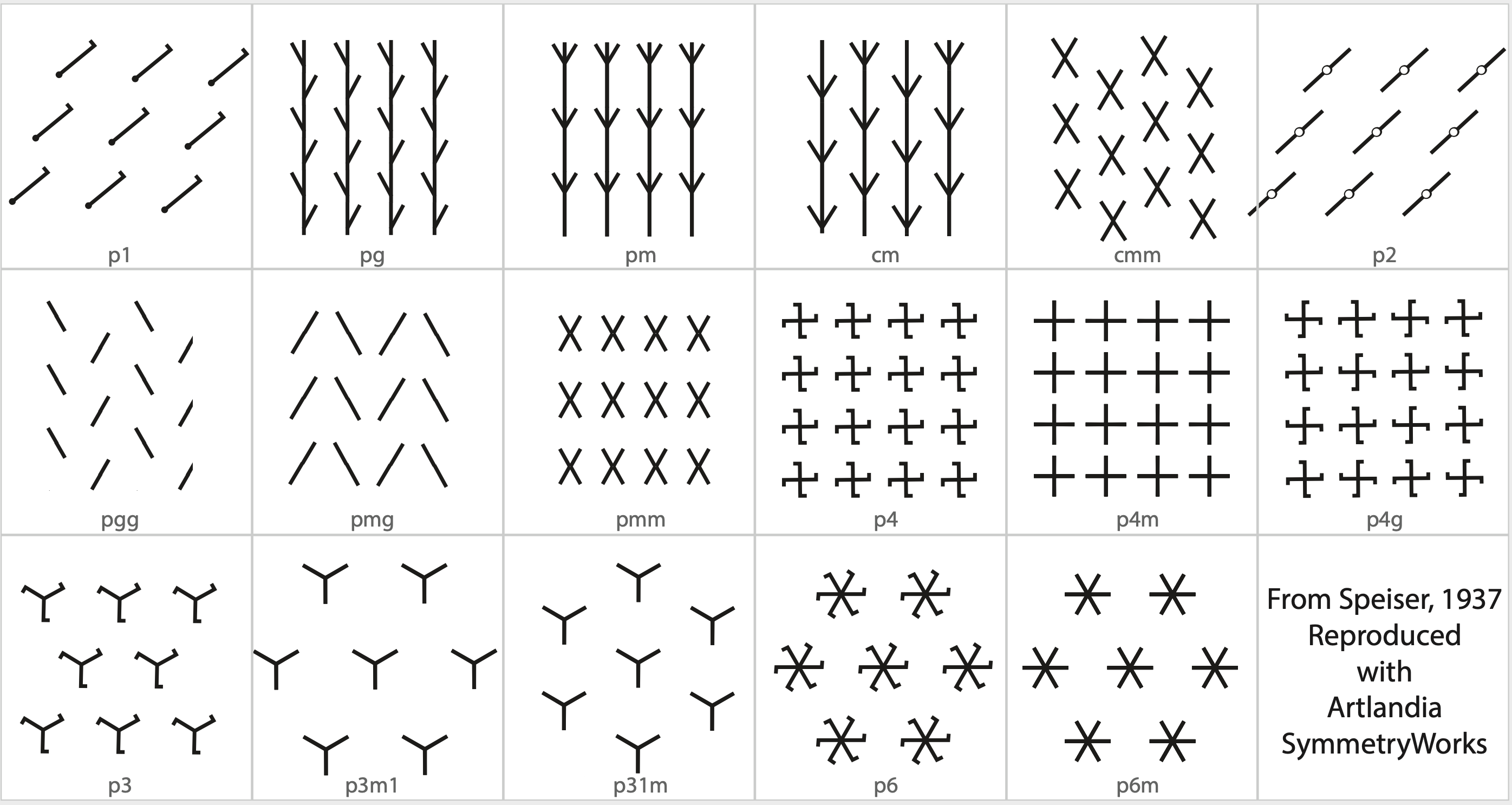
As a reminder, here are the 17 types of 2D crystallographic (wallpaper) symmetries. There are no others!
1. Readings on Pattern
Please read the following two book excerpts:
- Excerpt (Chapter 30, p. 64-81) from 10 PRINT, by Nick Montfort et al. [6MB PDF]
- Excerpt (Chapter 1, p. 17-37) from Graphic Games, by Victor Baumgartner, paying special attention to “Game C” [22MB PDF]
In a blog post, write a very brief response to something that you found interesting or helpful. Title your blog post, Nickname-PatternReading, and Categorize your post, 06-PatternReading.
Optional Inspirational Browsing:
- Check out The Grammar of Ornament (1856) by Owen Jones, one of the most gorgeous books ever published.
- Check out the fantastic Historic New England Wallpaper Archive, which has more than 6000 high-resolution scans of antique wallpapers.
- Check out the Experimental Pattern Sourcebook : 300 Inspired Designs from Around the World , by Jackie Herald, available online in CMU’s library.
- Browse the amazing Tilings and Patterns book by Grünbaum and Shephard. You can find a PDF copy online here, and there are two copies in the STUDIO (which don’t leave the room, please). This book includes many inspirational illustrations, such as these:
2. A Tiling Pattern Composition (Plotted)
Plotting out some multi-scale truchet patterns in the studio tonight. I'm kinda digging it more with lines missing — what do you think #plottertwitter ? pic.twitter.com/30BAxZcSlh
— Madeline Gannon (@madelinegannon) April 29, 2021
The purpose of this prompt is to strengthen your skills in generative form-making with modular design elements.
Making procedural patterns is a mental exercise in finding minimal reusable elements. This practice is old; we as a species have been using grids and patterns to decorate textiles, floors and borders of objects for a long time: from meander patterns in ancient Greece, to Chinese lattice design, the pleasure of repetition and variation catches our imagination. Take some time to look at decorative patterns and see how artists and designers have a long history of navigating the fine edge between the predictability of order and the surprise of variation and chaos. From Arabic geometrical patterns, to gorgeous African fabric designs, there is an entire universe of patterns to learn from.
— From the Book of Shaders by Patricio Gonzalez-Vivo.
Prompt: Develop a computationally-generated, machine-plotted artwork using tiling patterns—in which larger-scale structures appear to emerge from the arrangement of modular elements.
To create your project:
- Browse some of the examples from last Wednesday’s lecture. Consider the use of randomness. Consider algorithms like Truchet tiles, Wang tiles, Wave Function Collapse, etc. Some helpful tutorial videos can be found below. I have also provided some simple JS template code for generating Wang tiles.
- Sketch some ideas in your sketchbook. You are strongly encouraged to use more than one color in your design.
- Write code to generate pattern compositions. Export SVG files for plotting.
- Plot your artwork. Please do not use standard printer paper.
To document your project:
- Create a blog post on this website. Title your blog post, Nickname-TilingPattern, and Categorize your blog post, 06-TilingPattern.
- Embed some photographs of your sketches.
- Embed a good-quality photograph of your plotted composition. Consider having a second photograph showing a close detail.
- Write a paragraph (of about 100-150 words) describing the logic of your pattern, your sources of inspiration, your process, and an evaluation of your results. Be sure to acknowledge any code libraries that you used.
// Wang tiles in p5.js
var tiles;
var tileW, tileH;
var tileCols = 12;
var tileRows = 12;
function setup() {
createCanvas(600, 600);
tileW = width / tileCols;
tileH = height / tileRows;
tiles = create2DArray(tileRows, tileCols);
arrangeWithConstraints();
}
function mousePressed() {
arrangeWithConstraints();
}
function arrangeWithConstraints() {
for (var row = 0; row < tileRows; row++) {
for (var col = 0; col < tileCols; col++) {
var tileThis = 0;
if (row == 0 && col == 0) {
// The top-left tile is totally random.
tileThis = floor(random(16));
} else {
if (row > 0) {
var tileAbov = tiles[row - 1][col];
if ((tileAbov & 4) > 0) {
// If the tile above us points downwards,
// Draw upwards to connect with it.
tileThis += 1;
}
} else {
// For the first row,
// Draw upwards with some probability
if (random(1.0) < 0.333) {
tileThis += 1;
}
}
if (col > 0) {
var tileLeft = tiles[row][col - 1];
if ((tileLeft & 2) > 0) {
// If the tile to the left points to its right,
// Draw leftwards to connect with it.
tileThis += 8;
}
} else {
// For the first column,
// Draw leftwards with some probability
if (random(1.0) < 0.333) {
tileThis += 8;
}
}
if (random(1.0) < 0.6) {
// Draw downwards with some probability.
tileThis += 4;
}
if (random(1.0) < 0.2) {
// Draw rightwards with some probability.
tileThis += 2;
}
}
tiles[row][col] = tileThis;
}
}
}
function arrangeWithNoConstraints() {
// A purely random arrangement with no constraints.
for (var row = 0; row < tileRows; row++) {
for (var col = 0; col < tileCols; col++) {
var random4BitInt = floor(random(16));
tiles[row][col] = random4BitInt;
}
}
}
function draw() {
background(230);
for (var row = 0; row < tileRows; row++) {
for (var col = 0; col < tileCols; col++) {
var tileId = tiles[row][col];
var x = col * tileW;
var y = row * tileH;
push();
translate(x, y);
rect(0, 0, tileW, tileH);
drawTile(tileId);
pop();
}
}
}
function drawTile(id) {
var R = 20;
fill(0);
noStroke();
push();
translate(tileW / 2, tileH / 2);
ellipse(0, 0, R, R);
if ((id & 1) > 0) {
// draw upwards
rect(-R / 2, 0, R, -tileH / 2);
}
if ((id & 2) > 0) {
// draw rightwards
rect(0, -R / 2, tileW / 2, R);
}
if ((id & 4) > 0) {
// draw downwards
rect(-R / 2, 0, R, tileH / 2);
}
if ((id & 8) > 0) {
// draw leftwards
rect(0, -R / 2, -tileW / 2, R);
}
fill(255);
textAlign(CENTER, CENTER);
text(id, 0, 0);
pop();
}
function create2DArray(nrows, ncols) {
var arr = new Array(nrows);
for (var r = 0; r < nrows; r++) {
arr[r] = new Array(ncols);
}
return arr;
}