Category: 05-BlobFamily

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

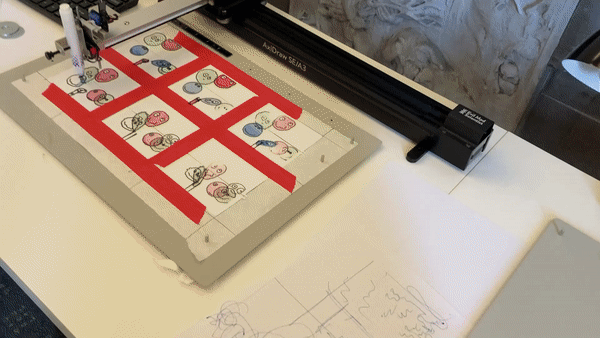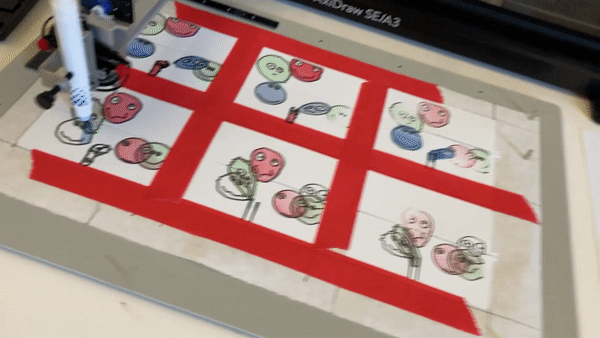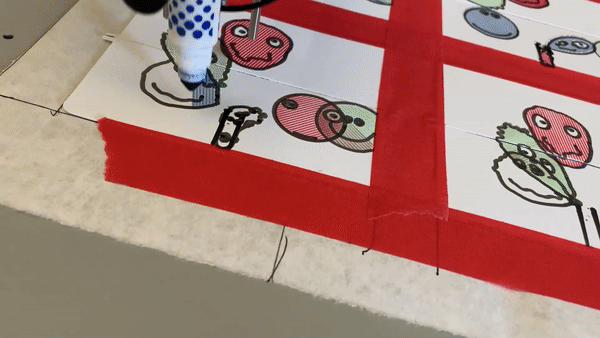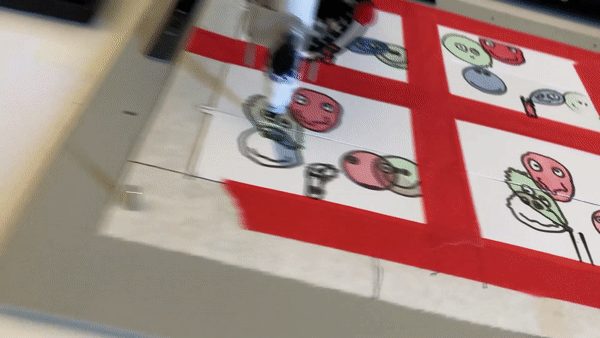
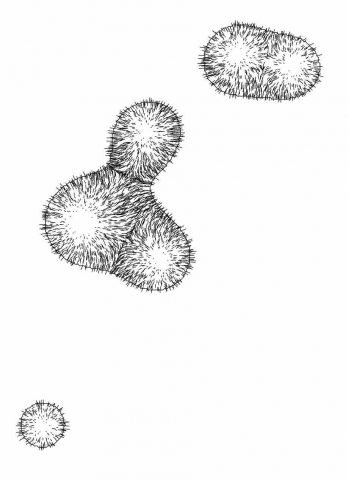
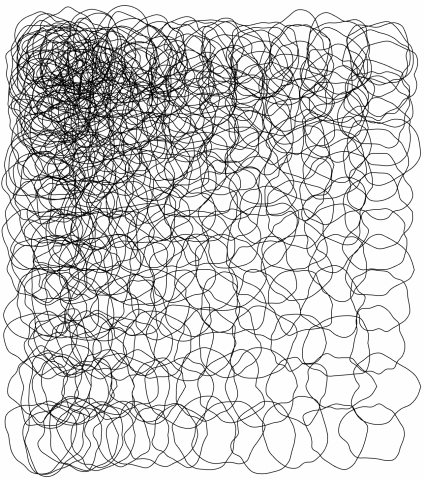
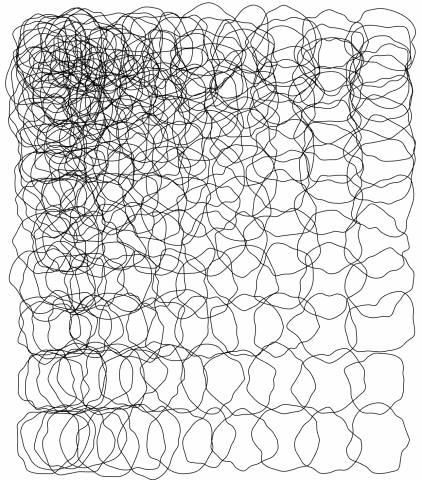
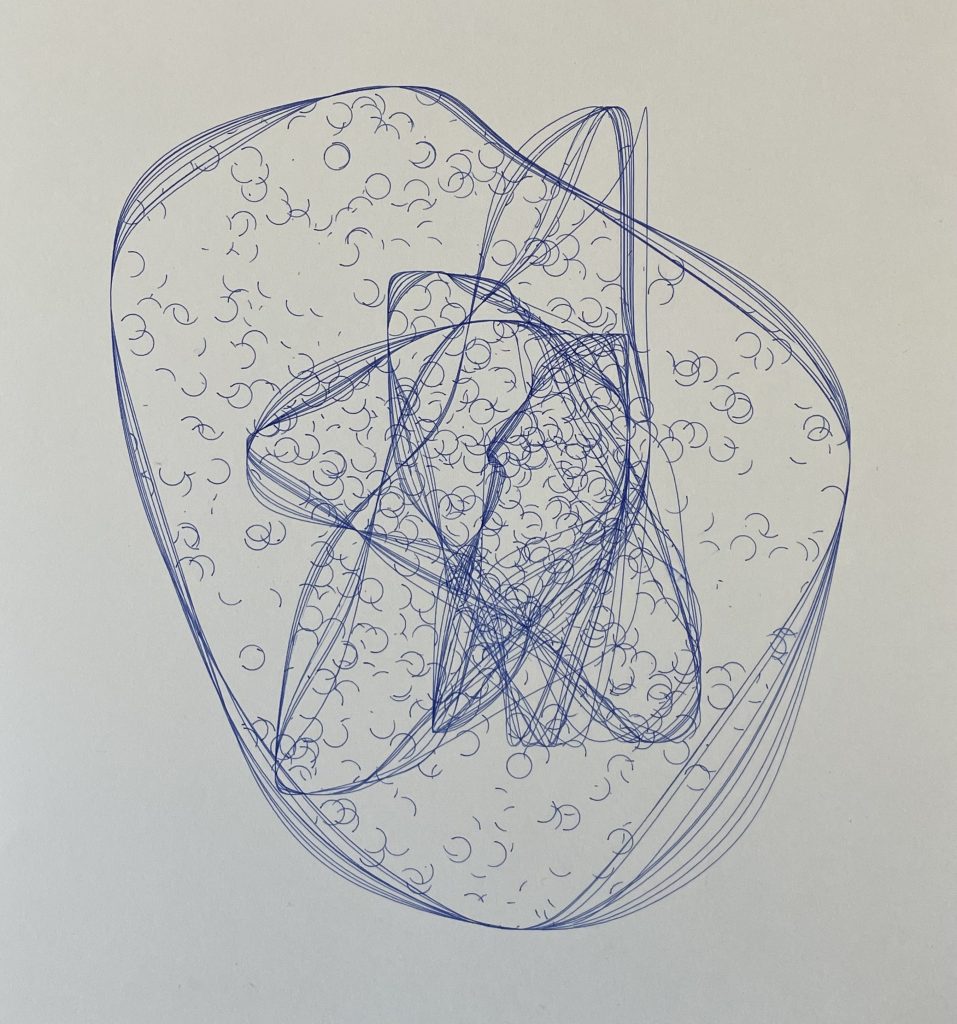
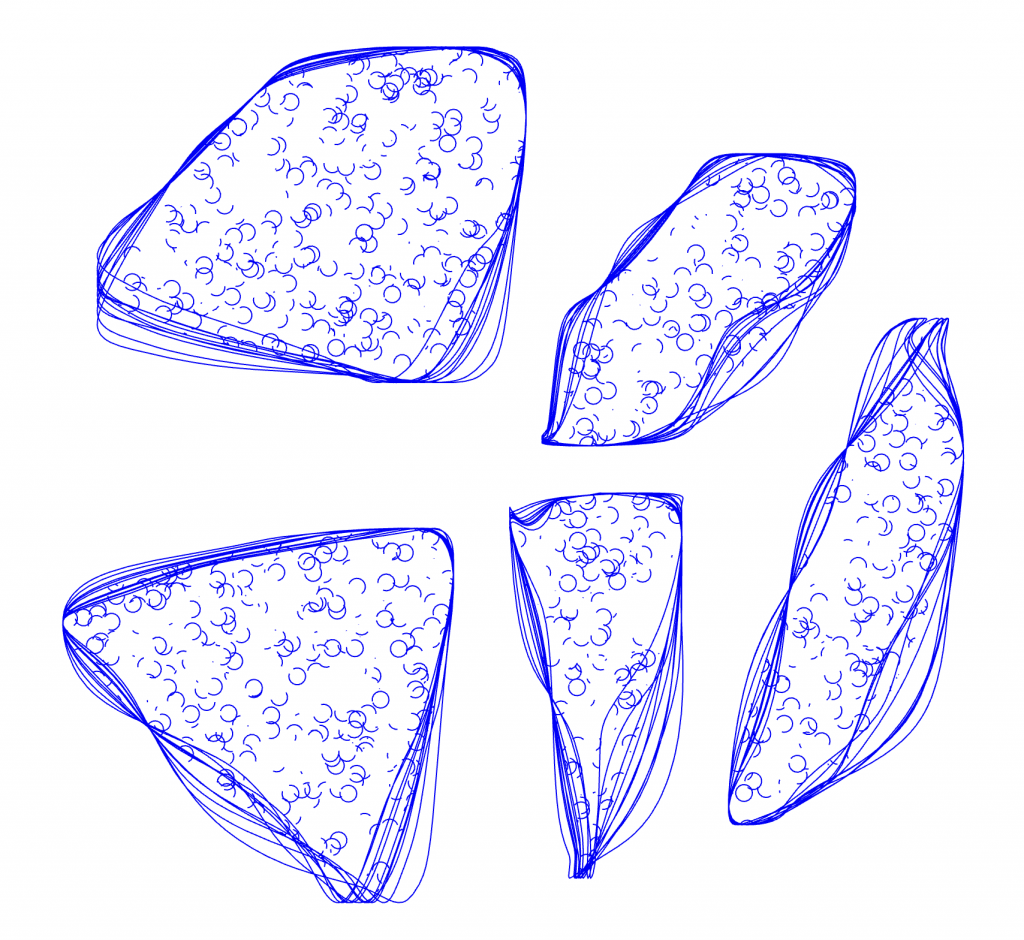
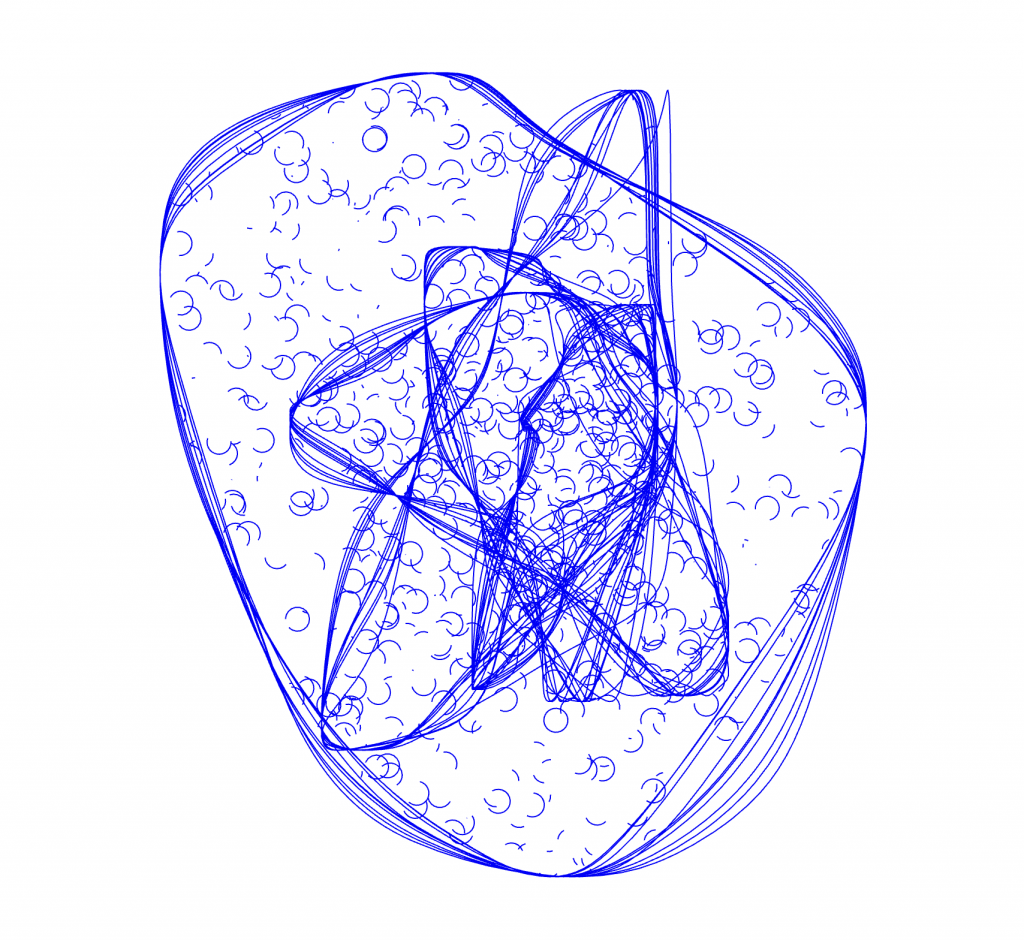
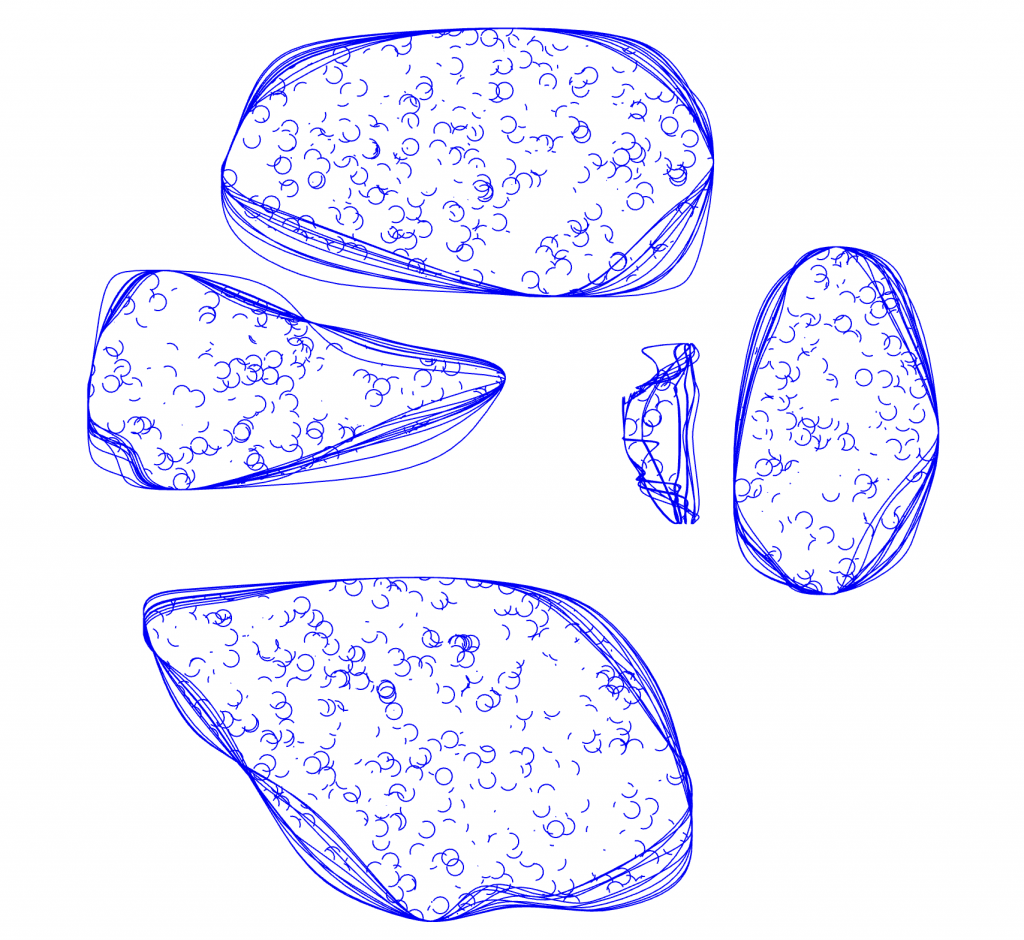
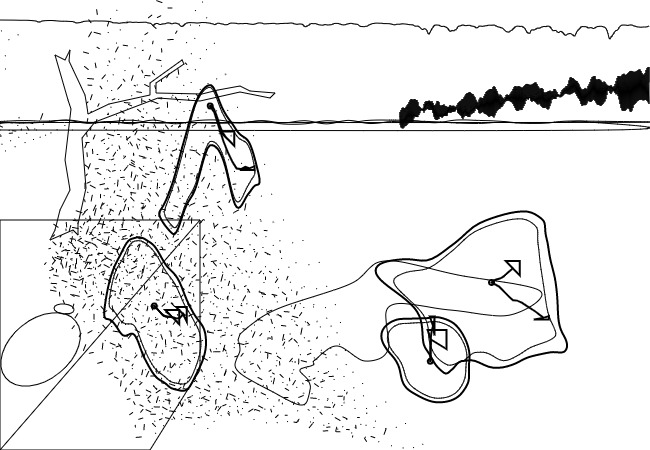
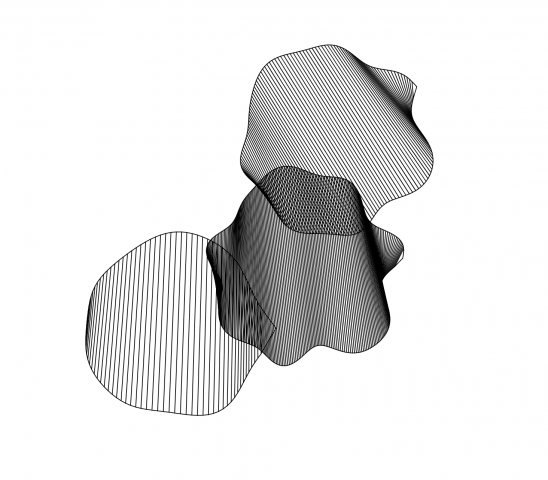
My interpretation of the blob family prompt manifested itself into an exploration of the differential growth algorithm. After dong some research on the algorithm itself and code tracing a few different implementations, I landed on Alberto Giachino’s Differential line growth with Processing. I have mostly been working in processing, and it didn’t require any outside dependencies, so it made the most sense to use this one as the base. Jason Webb’s 2D differential growth experiments also really helped in understanding how the algorithm works and how it can be modified. After playing around with the algorithm in the hatching exercise from last week, I wanted to see how I could constrain the growth to one specific shape, more specifically, in a blob-like shape. Golan had showed me how to use an off-screen graphics buffer, so I thought it might work if I tried to use that as a layer mask of sorts. The off-screen graphics buffer would contain white filled blobs (made by modifying the radius of a circle with perlin noise) against a black background. Therefore, whenever a node was at the location of a white fill, the differential growth cohesion and separation forces would act. When a node on the circle was at location of a black fill, there were no forces acting on it to make it grow. The nodes that were growing then formed into the shape of the blobs, and to my surprise, sort of collapsed in on each other where the edges were. It made what looked like the outline of the blob. The two pictures below are the blobs rendered digitally.

I had a lot of fun with this one! I love texture and I love organic/bodily looking things.

Here is the code:

Continue reading “bookooBread – BlobFamily”

I assembled a “flipbookit” which is a little contraption to play a 24 frame looping animation drawn on the backs and fronts of 24 cards. Originally, the animation loop was a series of smiley faces being slurped into a tube, but the way I shuffled around the cards it ended up being a bunch of smiley faces being spat out of a tube instead.

Each smiley is made up of four chains of springs and a bunch of repelling points: the spring chains make up the outline, two eyes, and a smile, and the whole face is filled with repelling points to give it some volume. Two of the points are selected to be the left and right pupils, respectively. The whole face is sucked into the tube with a force field that is applied to every point. There are also collisions with the tube walls.

Each of six faces is on its own 24 frame loop, and the loops are offset from each other by 4 frames. In order to exaggerate the acceleration of the faces as they are sucked into the tube, there are actually more sub-frame simulation steps towards the end of each individual 24 frame loop than in the beginning. It starts out with just a couple simulation steps on the first frame, and ends with several hundred on the last frame. The faces are also filled with a simple parallel-line hashing with three distinct colors.

Originally I planned the walls of the straw to be a thick outline, the outlines of the smileys to be thin pens, and the fill color to be cheap color markers. This all worked out except for the thin pens, which didn’t like to draw on the plastic-y surface of the flipbookit cards, so I ended up doing thick marker lines for all the lines. I suspect that this was actually a good thing, and helped by increasing readability of the animation, and by fudging some alignment errors both between the lines/colors within a frame as well as alignment between frames.

Each frame is drawn on two cards, the top half on one card and the bottom half on another card. Each card is printed on the front and back. Thus half of the cards have the top of an odd frame on one side and the bottom of an even frame of the other side; and the other half of the cards have the top of an even frame on one side and the bottom of an odd frame on the other side. Luckily I could fit twelve cards on a 11″ x 17″ AxiDraw, and there are two of those, so I could print all the odd frames at once, then flip all the cards over and shuffle them around and print all the even frames, with two AxiDraws in parallel. So two AxiDraws, front and back, black outlines and three colors, made for 2*2*4 = 16 distinct svgs (actually 2*2*5=20 cuz originally the straw outlines were separate from the smiley outlines). I figured flipping and taping down the cards was more of a pain than swapping markers, so I only flipped twice (once for each AxiDraw), and swapped markers 16 times.

Reading

“A blob is an illusion of controlled chaos” (Entering the Blobosphere, Laura Hyunjhee Kim). Is the illusion the control or the chaos? I imagine you could get different blobs by approaching it in both ways.

Hello!

Ever thought of making comics with code? I sure did! Hence why I decided to make this my blob assignment 😀

Continue reading “marimonda – blobfamily”

For mine I wanted to make hairy blobs.

here’s my blob

 

Continuing my practice of trying new tools for this course, I decided to try out the thing umbrella for this project. The umbrella is a project by Karsten Schmidt in which he creates a giant package ecosystem full of every algorithm one could ever want. Thi.ng was originally written in Clojure, and the transform definitely feels like Clojure. For instance, I spent a long time fighting with the system until I realized certain functions fail unless passed empty lists as a final parameter. That being said, the library is wildly powerful! I was able to achieve amazing results with very little code. I would totally use the thingiverse again, though maybe when under a much longer deadline. I found myself thinking of Good Shape while I worked—how it’s particularly difficult to describe what makes a shape “better.”

import { quad, asSvg, withAttribs, path } from '@thi.ng/geom';
import { star } from '@thi.ng/geom/ctors/polygon';
import { vertices } from '@thi.ng/geom/ops/vertices';
import { scatter } from '@thi.ng/geom/ops/scatter';
import { fuzzyPoly, compFill } from '@thi.ng/geom-fuzz';
import { svg } from '@thi.ng/hiccup-svg';
import { serialize } from '@thi.ng/hiccup';
import { shuffle } from '@thi.ng/arrays';

const width = 648;
const height = 864;

const buffer = 20;
const rad = 45;

const s = scatter(
    quad(
        [buffer + rad, buffer + rad],
        [width - buffer - rad, height - buffer - rad],
        [width - buffer - rad, height - buffer - rad],
        [0, height - buffer - rad],
    ),
    17,
);

const blobShapes = s.flatMap(([x, y], i) =>
    Array.from({ length: i % 2 ? 6 : 1 }, (_) =>
        star(
            rad + buffer * Math.random(),
            ~~(Math.random() * 5) + 3,
            [1.0, 1.5],
            {
                fill: 'none',
                stroke: 'black',
                'stroke-width': '1px',
                transform: `translate(${x},${y}) scale(${i / s.length})`,
            },
        ),
    ),
);
const blobs = blobShapes
    .map((s) =>
        fuzzyPoly(vertices(s), s.attribs, { jitter: 5, curveScale: 0.5 }),
    )
    .map((b) => withAttribs(b.children.at(0), b.attribs));

const scene = asSvg(...blobs);
const output = serialize(svg({ width, height }, scene));
document.querySelector('#app').innerHTML = `${output}`;

I have a somewhat meager offering for this week. I came up with another algorithm that combined circles with circular arcs by matching the slopes of the tangents, but I had difficulty implementing it. I was trying to mimic the forms of water bubbles, and it was going to look something like this:

I ended up pivoting to something simpler, an implementation of the algorithm that Golan mentioned in class, which mapped 2-d space Perlin noise to radial alteration of circles. I played a little bit with using the blobs to fill a space at different densities. Some of the different iterations looked like this:

 

I liked the poetry with which Laura Kim spoke about blobs, and how they saw blob-making as a form of alternative communication, a strange and novel language.

 

▲ ▲ ▲ ▲ ▲ PLOTS ▲ ▲ ▲ ▲ ▲

I created my blobs by bashing various Python libraries together. I used sklearn's SVM to get a 2D Voronoi classifier. Using that classifier I sorted random points into buckets and used scipy.spatial's ConvexHull algorithm to get a shapely LineString so that I could clip the hatching for later. I drew the actual curves using a modified version of Wikipedia's Catmull-Rom curve. To add the randomness to the edges I used a Perlin noise library to implement some approximation of p5.scribble. My inspiration was to create little potato creatures that were all holding hands (above). Due to time constraints I was only able to get the potato bodies. One thing I found interesting from the readings was the Town and Country salt and pepper shakers. I really vibed with the idea that blobs can be personified.

▼ ▼ ▼ ▼ ▼ GENERATOR ▼ ▼ ▼ ▼ ▼

 

One of the first things that came into my mind when we were assigned to create “blobs” for me was “what can a blob resemble”. After seeing a couple of blobs from the lecture, especially ones that illustrate a  “melting” kind of effect, I thought of Salvador Dali’s La Persistencia de la Memoria and the melting clocks within the painting. I didn’t realize how blobby those clocks actually were, but their form and shape were beautiful and were great representations of real objects turned “blobby”. My initial goal was to replicate the work, but realizing how difficult it was to get the details right, I decided to make a similar interpretation of the painting that alters that keeps the clock motif, and certain defining shapes in the painting, but simplifying a lot of the complicated forms. 

When converting to SVG mode in p5.js, I discovered that my code had a bug that existed and took me FOREVER to find. I ended up creating a more abstract version of the initial product, one that is more chaotic and I think diverges more from Salvador Dali’s painting. 

Sketches

Another SVG

Another SVG

Original Non-SVG version

Blob Reading Notes: 

In Laura Hyunjhee Kim’s A Blobafesto, I found the following line to be a great definition of how I see blobs: 

My initial idea of defining a blob was defining it by what it could not be, which was that it cannot have sharp edges, as it interferes with how we understand language and characterize words based on it’s pronunciation and syntax (I think this still somewhat stands true for me).

I really enjoyed the reading's introduction, where she mentions the term blobosphere and how it “transforms and transcends expectations from all shapes and forms”. I think this is also a phenomenal definition that I agree with, where the potentiality of blobs as a form seems to be endless, and that's the beauty of it. 

• I spent a lot of time trying to figure out how to make a blob with just my previous knowledge, but every attempt resulted in a very sharp-edged polygon that wouldn’t even come near the definition of a blob. I then decided to watch Dan Shiffman’s video on Perlin Noise loops; with that and the help of some smoothing done with averaging and noiseDetail() with Golan, I was able to create my blob family. The fill is not even in each blob, which resulted in a bendy look. I actually quite like how it looks because I think it adds some movement to the image.
• One thing that stuck out to me from Entering the Blobosphere reading was the de-categorization of the blob from the physical shape that it is so commonly associated with. In defining it as a conceptualization of progress and/or potential, its scope becomes much broader, and offers much more to contemplate.
• Here are some screenshots of my blobs:

Here is the SVG of my final blob family:

Here is the final plot: