Jamie – Page 2 – [OLD FALL 2017] 15-104 • Introduction to Computing for Creative Practice

jamieh-Looking-Outwards-07

Interaction between human and plants through lighting

The Botanicus Interacticus project by Disney Research (in collaboration with Philipp Schoessler, Jonas Loh/Studio NAND, Munehiko Sato) is an interactive technology that creates an expressive visual interaction between humans and plants. It was exhibited at the 2012 SIGGRAPH exhibition. The way the Botanicus Interacticus works is by placing a wire in the plant soil, which when touched or within close proximity with any location of the plant is detected, the collected data will trigger shapes and colours around the plant. Those shapes and colours depend on several factors, including touch/gesture, amount of contact and proximity. This project is based upon a sensing technology Touché, which was previously invented at Disney Research Pittsburgh. The added expression to the plants do not cause any harm and is non-invasive. The main purpose of the project was to eliminate the divide between real and artificial, which also develops new organic forms. My favourite aspect of this project is the response through lighting that dances around the plant based on interaction, which makes what is relatively static into something dynamic.

Computer showing the collected data of where touch is sensed

Below is a video of the interaction between person and plant.

jamieh-project-07-Curves

sketch

/*
Jamie Ho
jamieh@andrew.cmu.edu
10:30
Project 07
*/

var vals = 100;			//# of points to deltoidCrv
var angles = 360;		//total angle
var maxCrvs = 10;		//# of crvs desired

function setup() {
    createCanvas(450, 450);
}

function draw() {
	background(0);
	translate(width/2, height/2);
	
	for(var i = 0; i < maxCrvs; i++){
		//equal rotation of canvas for each drawDeltoidCrv based on # of crvs
		rotate(angles/i);	
		//stroke colour based on mouse position
		var colourX = map(mouseX, 0, width, 0, 255);
		var colourY = map(mouseY, 0, height, 0, 255);
		stroke(0, colourX, colourY);

		drawDeltoidCrv();
	}
}

function drawDeltoidCrv(){
	noFill();
	angleMode(RADIANS);
	beginShape();
	for(var i = 0; i < vals; i++){
		//mapping i to the circle
		var theta = map(i, 0, vals, 0, TWO_PI);		
		//multiplied factor for crvs
		var t = 60;									
		
		//making mouse positions a percentage to scale crvs
		var mX = map(mouseX, 0, width, 0, 1);		
		var mY = map(mouseY, 0, height, 0, 1);
		
		//defining x and y coordiantes of deltoid crv 
		//size of deltoid crvs are in relationship w/ mouse positions
		var x = (2*t*cos(theta)+t*cos(2*theta))*mX;	
		var y = (2*t*sin(theta)-t*sin(2*theta))*mY;	

		strokeWeight(0.5);
		vertex(x, y);
		line(0, 0, x, y);
	}
	endShape();
}

The curves are based on deltoid curves, which looks similar to a triangle. I experimented with using just the deltoid curve itself as well as representing the multiple curves with lines. Representing with lines look more interesting than just the deltoid curves themselves. I also experimented with where the lines are drawn from, such as from (0, 0) or from (width/2, heigth/2). Drawing lines from (width/2, height/2) makes the lines intersect in more complex ways, but I preferred how the 3 vertex ends of the curves are more dynamic with (0, 0) as starting point.

Final iteration with lines drawn from (0, 0) and vertexes of deltoid curves

Final iteration with size affected by mouse position

The hardest part of the process was incorporating the mouse position into the curves without messing up the shape, then I realized I could use mouse position by mapping it to make it a scale factor.

jamieh-LookingOutwards-06

http://iobound.com/pareidoloop/

Phil McCarthy created the project Pareidoloop, which combines a facial recognition algorithm with a random polygon generator algorithm to produce a somewhat recognizable face. The programs works by generating random sized, coloured and shaped polygons that are then layered on top of each other until the facial recognition algorithm recognizes a face. All other variables, except the random polygon generator, can be set by the user, such as size of image, fitness or how likely the “face” matches an actual face and number of generations. The maximum fitness level is 35, where the lower the number, the faster the image renders but the rendered face may not be recognizable. Number of generations is how many times the code runs until it stops to find another face. McCarthy was inspired by the idea of pareidolia, which is a when the mind responds to an image by perceiving a pattern within random data. An example of that would be objects in cloud formations or Pixar’s The Blue Umbrella short film.

Different possibilities to the pareidoloop code

There are certain user controlled variables, yet each time the code runs, the generated image is very different. There are so many different possibilities to this code. What I like about this project is how a face is a very defined image, but even when abstracted into simple polygons, from a distance, each face looks different from each other.

jamieh-Project06-Abstract-Clock

sketch

/*
Jamie Ho
jamieh@andrew.cmu.edu
10:30
Project 6
*/

var d1 = 24;	//hour
var d2 = 60;	//minutes/seconds
var slope1;		//slope of the diagonal line from hour triangle
var slope2;		//slope of the diagonal line from minute triangle

function setup() {
   createCanvas(200, 400);
}

function draw() {
	//this if statement inverts the black-white colours depending on AM or PM
	if(hour()>11){		//PM
		background(0);
	} else {			//AM
	background(255);
	}
//HOUR	
	slope1 = (height/2-height/8)/d1;
	for(var i = 0; i < d1; i++){
		//12am, 3am, 6am, 9am, 12pm, 3pm, 6pm, 9pm
		//longer and thicker line 
		if(i%3 == 0){
			if(hour()>11){
				stroke(200);
			} else {
			stroke(0);
		}
			strokeWeight(1);
			line(0, height/8+i*slope1,
			 	 width/2+d1-i, height/8+i*slope1);
		} else {
		//thin lines for all other times
			stroke(100);
			strokeWeight(0.5);
			line(0, height/8+i*slope1,
			 	 width/2-d1+i, height/8+i*slope1);
		}
		//blue triangle fill for HOUR
		noStroke();
		fill(26, 136, 255, 200);
		if(i == hour()){
			triangle(width/2+d1-i, height/8+i*slope1,
				 width/2-d1+i, height/8+i*slope1,
				 width/2, height/2);
		}
	}
//MINUTE
	slope2 = (height*(7/8)-height/2)/d2;
	for(var j = 0; j <= d2; j++){
		//10 min, 20 min, 30 min, 40 min, 50 min, 60 min
		if(j%10 == 0){			
			if(hour()>11){		//PM
				stroke(200);
			} else {			//AM
				stroke(0);
			}
			strokeWeight(1);
			line(width/2-j, height/2+j*slope2,
			 	 width, height/2+j*slope2);
		} 
		//blue quad fill for MINUTE
		noStroke();
		fill(0, 99, 204, 200);
		if(j == minute()){
			quad(width/2-d2, height*(7/8),
				 width/2+d2, height*(7/8),
				 width/2+d2-j, height*(7/8)-j*slope2,
				 width/2-d2+j, height*(7/8)-j*slope2);
		}
//SECOND
		stroke(179, 204, 255);
		strokeWeight(2);
		if(j == second()){
		line(width/2, height/2, width/2, height/2+j*slope2)
		}
	}
//TWO TRIANGLES
	if(hour()>11){		//PM
		stroke(255);
	} else {			//AM
		stroke(0);
	}
	strokeWeight(2);
	noFill();
	//hour triangle
	triangle(width/2-d1,height/8,
			 width/2+d1, height/8,
			 width/2, height/2);
	//minutes triangle
	triangle(width/2, height/2,
			 width/2-d2, height*(7/8),
			 width/2+d2, height*(7/8));
}

For this project, I wanted to do something similar to the hourglass, but make it more geometric with just triangles and lines. The lines and background colours invert when AM switches to PM and vice versa.

jamieh-Looking-Outwards-05

Diego Querol is a 3D artist and renders interior spaces as if the render itself was a photograph taken on site. He uses the modeling tool 3ds Max and rendering tool VRay to generate his renders. The entire process of generating an interior render starts from finding inspiration images on composition and details that could hint stories to modeling the interior pieces to adding textures and light. Within the process of rendering in VRay, the scale of the textures must match with reality and the multiple lighting options must be adjusted in a way that would enhance the rendering. For example, the scale of the pattern on the wood cannot be too big or small. And the treatment of glass and reflective surfaces because of the way light behaves on such surfaces (light is absorbed, transmitted and reflected on glass).

This type of artwork can bring a space to reality, which was once imagined. Querol also spends a lot of time and effort focusing on adding in details and filling the space with what is needed in order to convey a story or an atmospheric environment. This can be seen through his Arts and Crafts (below) rendered artwork, which is one of my favourite works of his.

jamieh-project-05-wallpaper

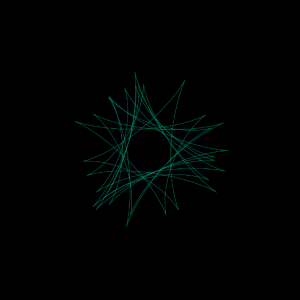
I first started with picking the colour palette for the background triangles, then took inspiration from cherry blossom trees and its changes over time with blue representing winter and pink representing summer.

sketch

/*
Jamie Ho
jamieh@andrew.cmu.edu
10:30
Project 5
*/

var SIZE = 50;
var c1x = 0; 	//top L (TL) corner X
var c1y = 0;	//top L (TL) corner Y
var c2x = 50;	//top R (TR) corner X
var c2y = 0;	//top R (TR) corner Y
var c3x = 0;	//bottom L (BL) corner X
var c3y = 50;	//bottom L (BL) corner Y
var c4x = 50;	//bottom R (BR) corner X
var c4y = 50;	//bottom R (BR) corner Y
var ratio = 0.5;
var ratio2 = 2/3;
var snow = 5;
var petal = 6;

function setup() {
    createCanvas(400, 350);
    background(0);
    
    noLoop();
}

function draw() {
	
	for(var h = 0; h < width/SIZE; h++){
		for(var v = 0; v < height/SIZE; v++){
			r = map(h, 0, width/SIZE, 155, 255);
  			b = map(v, 0, height/SIZE, 155, 255);

  			fill(r, b, b);
  			strokeWeight(0.5);
  			if(h < 4){									//Left half
	  			if(v%2 == 0){							//odd rows
					stroke(255);
					triangle(c1x+h*SIZE, c1y+v*SIZE,	//Right angle @ corner 1 (TL)
							 c2x+h*SIZE, c2y+v*SIZE,
							 c3x+h*SIZE, c3y+v*SIZE);	
					stroke(255);
					triangle(c2x+h*SIZE, c2y+v*SIZE,	//Right angle @ corner 4 (BR)
							 c3x+h*SIZE, c3y+v*SIZE,
							 c4x+h*SIZE, c4y+v*SIZE);
					push();
					//branches
					stroke(0);
					strokeWeight(0.5);
					line(c4x+h*SIZE, c4y+v*SIZE,
						 c4x*ratio+h*SIZE, c4y*ratio+v*SIZE);
					line(c2x*ratio*ratio+h*SIZE, c2y+v*SIZE,
						 c4x*ratio+h*SIZE, c4y*ratio+v*SIZE);
					line(c3x+h*SIZE, c3y*ratio*ratio+v*SIZE,
						 c4x*ratio+h*SIZE, c4y*ratio+v*SIZE);
					//snow
					noStroke();
					fill(255);
					ellipse(c2x*ratio*ratio+h*SIZE, c4y*ratio*ratio+v*SIZE, snow, snow);
					ellipse(c2x*ratio+h*SIZE, c4y*ratio*ratio*ratio+v*SIZE, snow*ratio, snow*ratio);
					ellipse(c2x*ratio*ratio2+h*SIZE, c4y-c4y*ratio*ratio+v*SIZE, snow, snow);
					
					//snow pile
					bezier(c3x+h*SIZE, c3y+v*SIZE,
						   c1x+c2x*ratio2*ratio+h*SIZE, c4y-ratio*ratio*ratio+v*SIZE,
						   c1x+c2x*ratio*ratio+h*SIZE, c4y-c4y*ratio*ratio2+v*SIZE,
						   c4x+h*SIZE, c4y+v*SIZE);
					pop();	

				} else {
					stroke(255);
					triangle(c1x+h*SIZE, c1y+v*SIZE,	//Right angle @ corner 2 (TR)
							 c2x+h*SIZE, c2y+v*SIZE,
							 c4x+h*SIZE, c4y+v*SIZE);	
					stroke(255);
					triangle(c1x+h*SIZE, c1y+v*SIZE,	//Right angle @ corner 3 (BR)
							 c3x+h*SIZE, c3y+v*SIZE,
							 c4x+h*SIZE, c4y+v*SIZE);

					push();
					//branches
					stroke(0);
					strokeWeight(0.5);
					line(c4x*ratio*ratio+h*SIZE, c4y+v*SIZE,
						 c4x*ratio+h*SIZE, c4y*ratio+v*SIZE);
					line(c2x+h*SIZE, c2y+v*SIZE,
						 c4x*ratio+h*SIZE, c4y*ratio+v*SIZE);

					//snow
					noStroke();
					fill(255);
					ellipse(c2x*ratio*ratio+h*SIZE, c4y*ratio*ratio+v*SIZE, snow*ratio, snow*ratio);
					ellipse(c2x*ratio+h*SIZE, c4y*ratio*ratio*ratio+v*SIZE, snow, snow);
					ellipse(c2x*ratio*ratio2+h*SIZE, c4y-c4y*ratio*ratio+v*SIZE, snow*ratio, snow*ratio);
					pop();
				}		


			} else {										//Right half
				if(v%2 != 0){								//odd rows						
						stroke(255);
						triangle(c1x+h*SIZE, c1y+v*SIZE,	//Right angle @ corner 1 (TL)
								 c2x+h*SIZE, c2y+v*SIZE,
								 c4x+h*SIZE, c4y+v*SIZE);	
						stroke(255);
						triangle(c1x+h*SIZE, c1y+v*SIZE,	//Right angle @ corner 4 (BR)
								 c3x+h*SIZE, c3y+v*SIZE,
								 c4x+h*SIZE, c4y+v*SIZE);

						push();
						//branches
						stroke(0);
						strokeWeight(1);
						line(c3x+h*SIZE, c3y*ratio*ratio+v*SIZE,
							 c4x*ratio+h*SIZE, c4y*ratio+v*SIZE);
						line(c3x+(c4x-c4x*ratio*ratio)+h*SIZE, c4y+v*SIZE,
							 c4x*ratio+h*SIZE, c4y*ratio+v*SIZE);

						//flower (EVEN)
						noStroke();
						fill(255, 102, 140);
						ellipse(c4x*ratio+h*SIZE, c4y*ratio+v*SIZE, petal/ratio, petal);
						ellipse(c4x*ratio+h*SIZE, c4y*ratio+v*SIZE, petal, petal/ratio);
						//white centre
						fill(255);
						ellipse(c4x*ratio+h*SIZE, c4y*ratio+v*SIZE, petal*ratio, petal*ratio);

						pop();

					} else {
						stroke(255);
						triangle(c3x+h*SIZE, c3y+v*SIZE,	//Right angle @ corner 2 (TR)
								 c2x+h*SIZE, c2y+v*SIZE,
								 c4x+h*SIZE, c4y+v*SIZE);	
						stroke(255);
						triangle(c1x+h*SIZE, c1y+v*SIZE,	//Right angle @ corner 3 (BR)
								 c3x+h*SIZE, c3y+v*SIZE,
								 c2x+h*SIZE, c2y+v*SIZE);

						push();
						//branches
						stroke(0);
						strokeWeight(1);						
						line(c1x+(c2x-c2x*ratio*ratio)+h*SIZE, c2y+v*SIZE,
							 c4x*ratio+h*SIZE, c4y*ratio+v*SIZE);
						line(c2x+h*SIZE, c4y*ratio*ratio+v*SIZE,
							 c4x*ratio+h*SIZE, c4y*ratio+v*SIZE);
						line(c3x+h*SIZE, c3y+v*SIZE,
							 c4x*ratio+h*SIZE, c4y*ratio+v*SIZE)

					//flower
						noStroke();
						fill(255, 102, 140);
						//centre flower (ODD)
						ellipse(c4x*ratio+h*SIZE, c4y*ratio+v*SIZE, petal, petal/ratio);
						ellipse(c4x*ratio+h*SIZE, c4y*ratio+v*SIZE, petal/ratio, petal);
						//on line flower
						ellipse(c1x+(c2x-c2x*ratio*ratio)+h*SIZE, c2y+v*SIZE, petal, petal/ratio);
						ellipse(c1x+(c2x-c2x*ratio*ratio)+h*SIZE, c2y+v*SIZE, petal/ratio, petal);
						//edge line flower
						ellipse(c2x+h*SIZE, c4y*ratio*ratio+v*SIZE, petal, petal/ratio);
						ellipse(c2x+h*SIZE, c4y*ratio*ratio+v*SIZE, petal/ratio, petal);
						//white centre
						fill(255);
						ellipse(c4x*ratio+h*SIZE, c4y*ratio+v*SIZE, petal*ratio, petal*ratio);
						ellipse(c1x+(c2x-c2x*ratio*ratio)+h*SIZE, c2y+v*SIZE, petal*ratio, petal*ratio);
						ellipse(c2x+h*SIZE, c4y*ratio*ratio+v*SIZE, petal*ratio, petal*ratio);
						pop();
					}		
				}
			}
	}
}

One of my challenges was trying keeping track of my variables, especially for the x and y coordinates of the corners that help me generate each triangle/square. I also had difficulty trying to shorten the code, which I know I can create my own function and call it, but I couldn’t figure out how to make sure it wouldn’t confuse my corner variables.

jamieh-Looking-Outwards-04

Volume, designed by Softlab, consists of a grid of 100 mirror panels that respond and redirect light and sound, as well as interact with human movement through depth cameras. The mirrors panels rotate to face the nearest person. Based on the volume of the ambient sound in the space, LEDs on the sides of the panels light up and the panels move vertically. The interface of the project was coded and built in Processing. Cameras are placed overhead to track people’s positions. The data is then managed with OCP and Arduino microcontrollers.

What I like about this project is how they took sound, which is intangible, and gave it spacial qualities through the rotation towards the person as well as quantitative information of the volume of the sound through the LED lights. Light and sound, which doesn’t seem to move, now visually circulate through space. I like that it reacts to human movement, but based on their description of the interface using the weighted average to find the closest person to the cube of mirrors makes me wonder what happens when there are more people who are standing close to the installation.

jamieh-Project-04-String-Art

Clicking the top and bottom grey bars changes the amount of lines and position of the lines.
Clicking the canvas flips the colours of the two different sets of lines.
Moving from quadrant to quadrant changes the line weights.

sketch

/*
Jamie Ho
jamieh@andrew.cmu.edu
10:30
Project 4
*/

var ratio;
var centreX;
var centreY;
var lines;
var t;


function setup() {
    createCanvas(400, 300); 

    ratio = 30;				//changes position of control points
    centreX = width/2;
    centreY = height/2;
    lines = 10;				//changes how how many divisions there are on the curve 
    						//which generates the white and blue lines 
}

function draw() {
	background(0);

	for (var i = 0; i <= lines; i++) {
	  t = i / lines;

	  //curve 1 from top L corner to mouse
	  c1x = curvePoint(mouseX, 0, mouseX, width/ratio*2, t);
	  c1y = curvePoint(mouseY, 0, mouseY, height/ratio*6, t);

	  //curve 2 from bottom L corner to mouse
	  c2x = curvePoint(mouseX, 0, width/ratio*6, width, t);
	  c2y = curvePoint(mouseY, height, mouseY, height/ratio*2, t);

	  //curve 3 from top R corner to mouse
	  c3x = curvePoint(width/ratio*2, width, mouseX, mouseX, t);
	  c3y = curvePoint(mouseY, 0, height/ratio*2, mouseY, t);

	  //curve 4 from bottom R corner to mouse
	  c4x = curvePoint(mouseX, width, width/ratio*6, 0, t);
	  c4y = curvePoint(mouseY, height, mouseY, height/ratio*6, t);

	  strokeWeight(1);
	  if(mouseX < centreX & mouseY < centreY){				//top L
			strokeWeight(0.15);
		} else if(mouseX > centreX & mouseY < centreY){	//top R
		  	strokeWeight(0.60);
		} else if(mouseX < centreX & mouseY > centreY){	//bottom L
		  	strokeWeight(0.30);
		} else {											//bottom R
		  	strokeWeight(0.90);
		}

	  if(mouseIsPressed){
		//white lines become blue
	  	stroke(204, 230, 255);
		  	line(c1x, c1y, c2x, c2y);
			line(c1x, c1y, c3x, c3y);
			line(c1x, c1y, c4x, c4y);
			line(c2x, c2y, c1x, c1y);
			line(c2x, c2y, c3x, c3y);
			line(c2x, c2y, c4x, c4y);
			line(c3x, c3y, c1x, c1y);
			line(c3x, c3y, c2x, c2y);
			line(c3x, c3y, c4x, c4y);

		//blue lines become white
		stroke("WHITE");
		  	line(c1x, c1y, c4y, c4x);
			line(c2x, c2y, c1y, c1x);
			line(c3x, c3y, c2y, c2x);
			line(c4x, c4y, c3y, c3x);

	  } else{
	  	//lines have different grey scales
	  	stroke(75);
			line(c1x, c1y, c2x, c2y);
			line(c1x, c1y, c3x, c3y);
			line(c1x, c1y, c4x, c4y);
		stroke(150);	  
			line(c2x, c2y, c1x, c1y);
			line(c2x, c2y, c3x, c3y);
			line(c2x, c2y, c4x, c4y);
		stroke(255);
			line(c3x, c3y, c1x, c1y);
			line(c3x, c3y, c2x, c2y);
			line(c3x, c3y, c4x, c4y);
		//blue lines
		stroke(0, 119, 230);
		  	line(c1x, c1y, c2y, c2x);
			line(c2x, c2y, c3y, c3x);
			line(c3x, c3y, c4y, c4x);
			line(c4x, c4y, c1y, c1x);
	  }
	}

		//the four rectangles here are for ease of seeing where to mouse click
		noStroke();
		fill(200, 200);
		rect(0, 0, width/2, 20);				
		rect(0, height-20, width/2, 20);		
		
		fill(200, 100);
		rect(width/2, 0, width, 20);
		rect(width/2, height-20, width, 20);

		stroke("RED");
		strokeWeight(1);
		//Up arrow
		line(width/4, 0, width/4, 20);	
		line(width/4-10, 10, width/4, 0);
		line(width/4+10, 10, width/4, 0);
		//Right arrow
		line(width/4*3-10, 10, width/4*3+10, 10);
		line(width/4*3, 0, width/4*3+10, 10);
		line(width/4*3+10, 10, width/4*3, 20);
		
		
		if(mouseIsPressed & mouseY < 20 && mouseX < width/2 && lines < 60){			//if click on top L bar
			lines += 1;																	//amt of lines increases to 59
		} else if(mouseIsPressed & mouseY > 280 && mouseX < width/2 && lines > 1){		//if click on bottom L bar
			lines -= 1;																	//amt of lines decreases to 1
		}

		if(mouseIsPressed & mouseY < 20 && mouseX > width/2){							//if click on top R bar
			ratio -= 1;																	//lines shift right
		} else if(mouseIsPressed & mouseY > 280 && mouseX > width/2){					//if click on bottom R bar
			ratio += 1;																	//lines shift left
		}
}

The hardest part was trying not to repeat code, which I had trouble with in the for loop to achieve the effect of what happens when mouse is pressed.

jamieh-LookingOutwards-03

The Silk Pavilion by the MIT Media Lab consists of 26 polygonal panels and silk threads woven by a CNC (computer-numerically controlled) machine. The algorithm used to weave out the silk threads was based upon study of silk worms, their natural behavior and how they use something 2-dimensional to create a space that is 3-dimensional. The shape of the pavilion uses an algorithm that uses a continuous thread to weave the panels with differing degrees of density. Once the machine-aspect of the pavilion was finished, 6500 silkworms were placed onto the pavilion was to bring in the natural aspect by allowing them to reinforce any gaps neglected by the CNC machine.

This project is a synthesis between man-made, digital form and natural form. It’s introducing something controlled to the natural environment and introducing something natural to the machine. What is also admirable about this project is the focus on studying the silkworms and its natural instincts, which the team was able to transfer into code for the machine to develop an architecture for the silkworms.

jamieh-Project-03-Dynamic-Drawing

sketch

/*
Jamie Ho
10:30
jamieh@andrew.cmu.edu
Project 03
*/

var rectSize = 10;
var d = 75; //distance from edges and distance between each rectangle's corner

function setup() {
    createCanvas(640, 480);
    rectMode(CORNER);
    angleMode(DEGREES);
}

function draw() {
    background(0);
    fill(256);
    
    //to create array of rectangles
    for(var x = 0+d; x <= width-d; x+=d){
        for(var y = 0+d; y <= height-d; y+=d){
            
            //dis = distance between mouse pointer and rectangle
            var dis = dist(x, y, mouseX, mouseY);
            var inCanvas = d < mouseX & mouseX < width-d && d < mouseY && mouseY < height-d;
                
                
        //CHANGING COLOURS
            //if rectangles are far from mouse: rectangles are white
            //far = more than half the width of canvas
            if(dis > width/2 & inCanvas){            
                fill(256, 256, 256);
            }

                //if rectangles are close from mouse: rectangles flash in colour
                //close = less than half the width of canvas
                else if(dis < width/2 & inCanvas){
                    fill(random(0, 256),random(0, 256),random(0, 256));
                }


        //ROTATING + TRANSLATION
            
            //Top L = "starting point" 
                //no rotation no translation no shear, just size change
            
            //Top R = rotates a bit
            if(mouseX > width/2 & mouseY < height/2 && inCanvas){
                rotate(random(-0.05, 0.05));
            }

            //Bottom R = rotates double of Top R + translates
            if(mouseX > width/2 & mouseY > height/2 && inCanvas){
                rotate(random(-0.1, 0.1));
                translate(x*random(0.005, 0.0075), y*random(0.005, 0.0075));
            }

            //Bottom L = rotates quadruple of Top R/double of Bottom R + translates + shears
            if(mouseX < width/2 & mouseY > height/2 && inCanvas){
                rotate(random(-0.2, 0.2));
                translate(x*random(0.005, 0.0075), y*random(0.005, 0.0075));
                shearX(PI/16);
            }




        //CHANGING SIZE
            //if mouse is within borders of "new" canvas, 
            //then rectangles change size based on distance of pointer to rectangle
            if(inCanvas){
                rect (x, y, dis*0.1, dis*0.1);
            }

                //if mouse is not within canvas, then rectangles are small AND rotates
                else{
                    rect (x, y, rectSize, rectSize)

                }

        }
    }
   
}

For this project, I made use of for loops to create an array of the same shapes, then used conditional statements to make modifications. The dynamic drawing starts off static with the original rectangles, but when the mouse moves, the rectangles change in size based on each of their distances from the mouse. When the mouse moves into a different quadrant, the rectangles react differently through rotation, translation, shear. From the top left quadrant to the bottom left quadrant (clockwise), the movements to the rectangles become more dramatic. The hardest parts of this project were making the for loop work, making sure the conditional statements made sense and adjusting the numbers assigned to variables to an appropriate range so that the shapes appear on canvas.