Category: Project-07-Curves

sketch

/*
Connor McGaffin
Section C
cmcgaffi@andrew.cmu.edu
Project-07
*/
var nPoints = 1;
var x;
var y;

function setup() {
    createCanvas(480, 480);
}

//--------------------------
function draw() {
    background(250);
    angleMode(DEGREES);

    //top row
    push();
    rotate(1 * mouseX / 2);
    cardioids();
    pop();

    push();
    translate(width / 2, 0);
    rotate(1 * mouseX / 2);
    cardioids();
    pop();

    push();
    translate(width, 0);
    rotate(1 * mouseX / 2);
    cardioids();
    pop();

    //middle row
    push();
    translate(0, height / 2);
    rotate(1 * mouseX / 2);
    cardioids();
    pop();

    push();
    translate(width / 2, height / 2);
    rotate(1 * mouseX / 2);
    cardioids();
    pop();

    push();
    translate(width, height / 2);
    rotate(1 * mouseX / 2);
    cardioids();
    pop();

    // bottom row
    push();
    translate(0, height);
    rotate(1 * mouseX / 2);
    cardioids();
    pop();

    push();
    translate(width / 2, height);
    rotate(1 * mouseX / 2);
    cardioids();
    pop();

    push();
    translate(width, height);
    rotate(1 * mouseX / 2);
    cardioids();
    pop();


}

function cardioids(){

    var mY = constrain(mouseY, width / 4, width / 2) * .4;
    var a = mY;
    
    noStroke(0);

    //horiz axis
    //pink
    beginShape();
    fill('rgba(250, 100, 250, 0.6)');
    for(i = 0; i < 360; i++){
        var t = map(i, 0, nPoints, 0, nPoints);
        x = a * sin(t) * (1 - sin(t));
        y = a * cos(t) * (1 - sin(t));
        vertex(x, y);
    }
    endShape(CLOSE);
    //dark blue
    beginShape();
    fill('rgba(10, 100, 250, 0.6)');
    for(i = 0; i < 360; i++){
        var t = map(i, 0, nPoints, 0, nPoints);
        x = a * sin(t) * (1 - sin(t));
        y = a * cos(t) * (1 - sin(t));
        vertex(-x, -y);
    }
    endShape(CLOSE);

    //vert axis
    //rotate 90
    push();
    rotate(90);
    //light blue
    beginShape();
    fill('rgba(50, 150, 220, 0.6)');
    for(i = 0; i < 360; i++){
        var t = map(i, 0, nPoints, 0, nPoints);
        x = a * sin(t) * (1 - sin(t));
        y = a * cos(t) * (1 - sin(t));
        vertex(x, y);
    }
    endShape(CLOSE);
    //
    beginShape();
    fill('rgba(180, 10, 250, 0.6)');
    for(i = 0; i < 360; i++){
        var t = map(i, 0, nPoints, 0, nPoints);
        x = a * sin(t) * (1 - sin(t));
        y = a * cos(t) * (1 - sin(t));
        vertex(-x, -y);
    }
    endShape(CLOSE);

    //white hub
    //fill(250);
    //ellipse(0, 0, a * .6, a * .6);

    pop();
}








    

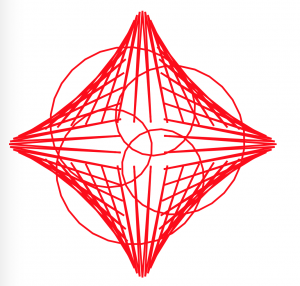
This project was tricky. I definitely would have struggled a lot more if I didn’t have the example code in the project brief, but once I found a curve I was drawn to and started plugging variables in for interaction, the project became a playful process.

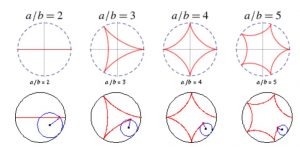
I used s series of cardioid curves to create small pinwheel like elements, which I then organized in rows and columns on the screen. Moving the mouse up and down will scale the pinwheels, whereas moving side to side changes its direction.

I hope to revisit this code, because I know that there are ways to display it in a more compact way and achieve similar results. This is one of the few projects thus far that I feel genuinely proud of its final product.

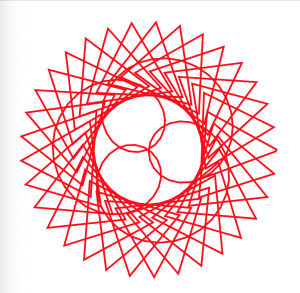
Below are screenshots of earlier iterations, when I was still figuring out color palettes and general composition of my canvas.

Project

/*Sharon Yang
Section C
junginny
Project-07
*/

var nPoints = 100;

function setup() {
  createCanvas(480, 480);
}

function draw() {
  background(254, 200, 200);
  push();
  translate(width/2, height/2);
  rotate(PI); //rotating the shape 180 degrees
  drawHeart(); //call the function to draw the shape
  pop();
}

function drawHeart() { //function to create the heart shape
  noStroke();
  if (mouseX <= 240 & mouseY <= 240) { //the mouse X and Y determines the color of the shape
    fill(255, 0, 0); //red
  }
  else {
    fill(200, 25, 60); //burgundy
  }
  beginShape(); //create the heart shape
  for (var i = 0; i < nPoints; i++) {
    var t = map (i, 0, nPoints, 0, TWO_PI);
    var consMouseX = constrain(mouseX,0,width/2);
    var consMouseY = constrain(mouseY,0,height/2.2);//constrain to stay within the canvas border 
    x = 16 * pow(sin(t), 3);
    y = 13 * cos(t) - 5 * cos(2 * t) - 2 * cos(3 * t) - cos(4 * t); //formula for the shape
    x = map(x,0,16,0,consMouseX);
    y = map(y,0,16,0,consMouseY);
    vertex (x, y)
  }
  endShape(CLOSE);
}

This project was particularly difficult to start as a mathematical equation also had to be incorporated for the geometric shape. However, once making the shape with begin and end shape, it was quite straightforward to make the shape increase and decrease in size and make the color change with mouse X and Y. The following are the screenshots of the varying image with different mouse X and Y.

Project 07 Curves

This project was super interesting to make and play with. Some of the math involved with the manipulation of more complex curves eluded me a little. However, I found overlaying the Dumbbell Curve and Devil Curve to be really pleasing to spin around and mess with the sizing of them. This was a difficult assignment and I wish I could’ve para-metricized the curves more into a perspective or abstract three dimensional volumes. This project looks really flat and I think after more practice I would like to impose more perspective lines and curves that reach beyond the canvas in a more interesting composition.

The Dumbell Curves make nice looking clover shapes that have some hidden shapes behind it from the Devil’s Curve.

sketch

//Sean McGadden
//smcgadde@andrew.cmu.edu
//Project 07
//Section C

 
//Drawing Setup
function setup() {
    createCanvas(640, 400);
    
}

//Chosing to call from curveX or curveY
function draw() {
  background(160, 190, 255);
    push();
    translate(width / 2, height / 2);
    drawCurve(false, false);
    drawCurve(false, true);
    drawCurve(true, true);
    drawCurve(true, false);
    pop();    
}

//Drawing Dumbell Curve 
//basic varible defintion and instantiation of Dumbell Curve
function drawCurve(isDumbell, isFlipped) {
    
    var x;
    var y;
    var nPoints = 100;
    
    var percX = mouseX / 640.0;
    var percY = mouseY / 400.0;
    rotate(TWO_PI * percY);
    
    var a = 200.0 * percX;
    var t 
    
    stroke("lightcyan");
    fill("green");
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        
        x	=	curveX(isDumbell, a, t);
        y	=	curveY(isDumbell, a, t);
        
        if (isFlipped) {
            var temp = x;
            x = y;
            y = temp;
        }
        vertex(x, y);
    }
    endShape(CLOSE);
}

//Returns x value of the desired curve
//Choosing between Dumbell Curve or the Devil's Curve based on a and t
//Devil's Curves uses thrid variable called b initialized below
function curveX(isDumbell, a, t) {
    if(isDumbell){
        return a * sin ( t);
    } else {
        var b = a / 2.0;
        return cos(t) * sqrt(((a * a * sin(t) * sin(t))-(b * b * cos(t) * cos(t)))/((sin(t) * sin(t)) - (cos(t) * cos(t))));
    }
    
}
//Returns y value of the desired curve
//Choosing between Dumbell Curve or the Devil's Curve based on a and t for the 
//Devil's Curves uses thrid variable called b initialized below
function curveY(isDumbell, a, t) {
    if(isDumbell){
        return a * sin(t) * cos(t);
    } else {
        var b = a / 2.0;
        return sin(t) * sqrt(((a * a * sin(t) * sin(t))-(b * b * cos(t) * cos(t)))/((sin(t) * sin(t)) - (cos(t) * cos(t))));
    }
}

Sean McGadden

sketch

// Christine Seo
// Section C
// mseo1@andrew.cmu.edu
// Project-07

var leftColor;
var rightColor; 
var inBetweenColor;
var scaledVal;

function setup() {
  createCanvas(450, 450);
  rightColor = color(249, 185, 226); 
  leftColor = color(226, 213, 248); 
  inBetweenColor = color(182, 115, 138);
  scaledVal = 0; 
  strokeColor = 0;

}

function draw() {
  background(0);
  translate(width / 2, height / 2); //drawing is place to the center of canvas
  Hypotrochoid();
  angleMode(DEGREES);
}

function Hypotrochoid() {
    scaledVal = map(mouseX, 0, width, 0,1);  //color of the strokes change from left to right
    inBetweenColor = lerpColor(leftColor, rightColor, scaledVal);
    noFill();
    stroke(inBetweenColor);
     if (mouseX < (width / 1.5)) {
      stroke(strokeColor);
      strokeColor = map(mouseX, 0, width, 0, 255);
    }

    var x;
    var y;
    var x2;
    var y2;
    var c = constrain(mouseX, 50, 10, width); //constrained distance of the radius of the circles 
    var r = 175; //radius of outter circle
    var r2 = 5; //radius of inner circle 
    var b = r / constrain(mouseY, 50, height);  //constrained radius of small circles

    beginShape();
     for (var i = 0; i < r; i ++) {

     var t = map(i, 10, r, 10, 360);

     var x = (r + b) * cos(t) - c * cos (((r + b) / b) * t); //Hypotrochoid equation (outter circle)
     var y = (r + b) * sin(t) - c * sin (((r + b) / b) * t);
     var x2 = (r2 + b) * cos(t) - c * cos (((r2 + b) / b) * t); //inner circle
     var y2 = (r2 + b) * sin(t) - c * sin (((r2 + b) / b) * t);
           
     vertex(x, y); //outter circle
     vertex(x2, y2); //inner circle
        }  

    endShape();
}

For this project, I loved exploring all the variety of shapes and forms that the Hypotrochoid function could make. Although the mathematical equations seemed difficult at first, I was able to successfully make intriguing shapes that I wanted to create. I also explored to make colors of the strokes change using the mouse. I have two different sets of Hypotrchnoid in the project, that gives the overall product to have a “core” in the middle of the canvas. If you move the mouse more slowly, you are able to see that there are a lot of different shapes that can be made through your mouse. I found out that the constrain function is very useful in this project and for future projects as well. It is really interesting how it looks like the shapes are rotating consistently; I definitely want to explore more functions such as Hypotrochoid and epitrochoid.