emadayflames
//Elizabeth Maday
//Section A
//emaday@andrew.cmu.edu
//Project 7
var nPoints = 450;
//background color
var r = 0;
var g = 0;
var b = 0;
//red fire colors
var r1 = 255;
var b1 = 0;
var g1 = 0;
var r2 = 255;
var g2 = 85;
var b2 = 0;
var r3 = 255;
var g3 = 164;
var b3 = 0;
var r4 = 255;
var g4 = 204;
var b4 = 0;
//blue fire colors
var R1 = 7;
var G1 = 83;
var B1 = 130;
var R2 = 27;
var G2 = 125;
var B2 = 186;
var R3 = 73;
var G3 = 174;
var B3 = 237;
var R4 = 105;
var G4 = 185;
var B4 = 234;
//shadow colors red
var rr = 108; //inside
var gg = 22;
var bb = 0;
var rrr = 255;//outside
var ggg = 58;
var bbb = 0;
//shadow colors blue
var RR = 4; //inside
var GG = 22;
var BB = 33;
var RRR = 22; //outside
var GGG = 63;
var BBB = 89;
//water colors blue
wr = 47;
wg = 102;
wb = 191;
//water colors green
WR = 12;
WG = 201;
WB = 72;
function setup() {
createCanvas(400, 400);
frameRate(6);
strokeWeight(0.7);
}
function mouseClicked() {
if (r1 === 255) {
r1 = R1;
g1 = G1;
b1 = B1;
r2 = R2;
g2 = G2;
b2 = B2;
r3 = R3;
g3 = G3;
b3 = B3;
r4 = R4;
g4 = G4;
b4 = B4;
r = 4;
g = 22;
b = 70;
rr = RR;
gg = GG;
bb = BB;
rrr = RRR;
ggg = GGG;
bbb = BBB;
wr = WR;
wg = WG;
wb = WB;
} else if (r1 === 7) {
r1 = 255;
g1 = 0;
b1 = 0;
r2 = 255;
g2 = 85;
b2 = 0;
r3 = 255;
g3 = 164;
b3 = 0;
r4 = 255;
g4 = 204;
b4 = 0;
r = 0;
g = 0;
b = 0;
rr = 108;
gg = 22;
bb = 0;
rrr = 255;
ggg = 58;
bbb = 0;
wr = 47;
wg = 102;
wb = 191;
}
}
function draw() {
background(r, g, b);
translate(200, 200);
shadows(0, 0);
fire(0, 0);
water2(0, 0);
textSize(15);
text('Click!', -170, 170);
}
function shadows(x, y) {
translate(x, y);
push();
ellipseMode(CORNER);
fill(rrr, ggg, bbb); //outside
ellipse(-35, 5, random(125, 130), random(40, 50));
fill(rr, gg, bb); //inside
ellipse(-25, 5, 70, random(20, 30));
pop();
}
function fire(x, y) {
translate(x, y);
beginShape();
fill(r1, g1, b1);
//outermost part
for (var i = 0; i < nPoints; i += 1) {
var num = random(1, 1.4);
var r = num - sin(theta);
var theta = map(i, 0, nPoints, 0, TWO_PI);
var grow = (dist(mouseX, mouseY, width/2, height/2))/3.5;
var x = grow * (r*cos(theta));
var y = grow * (r*sin(theta));
vertex(x, y);
}
endShape(CLOSE);
//second to outermost part
beginShape();
fill(r2, g2, b2);
for (var i = 0; i < nPoints; i += 1) {
var num = random(0.9, 1.2);
var r = num - sin(theta);
var theta = map(i, 0, nPoints, 0, TWO_PI);
var grow = (dist(mouseX, mouseY, width/2, height/2))/3.5;
var x = grow * (r*cos(theta));
var y = grow * (r*sin(theta));
vertex(x, y);
}
endShape(CLOSE);
//second to innermost part
beginShape();
fill(r3, g3, b3);
for (var i = 0; i < nPoints; i += 1) {
var num = random(0.6, 1);
var r = num - sin(theta);
var theta = map(i, 0, nPoints, 0, TWO_PI);
var grow = (dist(mouseX, mouseY, width/2, height/2))/3.5;
var x = grow * (r*cos(theta));
var y = grow * (r*sin(theta));
vertex(x, y);
}
endShape(CLOSE);
//innermost part
beginShape();
fill(r4, g4, b4);
for (var i = 0; i < nPoints; i += 1) {
var num = random(0.2, 0.5);
var r = num - sin(theta);
var theta = map(i, 0, nPoints, 0, TWO_PI);
var grow = (dist(mouseX, mouseY, width/2, height/2))/3.5;
var x = grow * (r*cos(theta));
var y = grow * (r*sin(theta));
vertex(x, y);
}
endShape(CLOSE);
}
function water2(x, y) {
translate(x, y);
fill(wr, wg, wb);
for (var i = 0; i < nPoints; i += 1) {
var x = dist(mouseX, mouseY, width/2, height/2) * 1.2;
var y = dist(mouseX, mouseY, width/2, height/2) * 1.2;
var size = dist(mouseX, mouseY, width/2, height/2)/4;
ellipse(x, y, size, size);
push();
fill(255);
ellipse(x - 2, y, size - (size*0.6), size - (size*0.6));
pop();
var x1 = (dist(mouseX, mouseY, width/2, height/2)) * -1;
var y1 = dist(mouseX, mouseY, width/2, height/2);
var size1 = dist(mouseX, mouseY, width/2, height/2)/5;
ellipse(x1, y1, size1, size1);
push();
fill(255);
ellipse(x1 - 2, y1, size1 - (size1*0.6), size1 - (size1*0.6));
pop();
var x2 = (dist(mouseX, mouseY, width/2, height/2)) * -1.2;
var y2 = (dist(mouseX, mouseY, width/2, height/2)) * -1.2;
var size2 = dist(mouseX, mouseY, width/2, height/2)/4;
ellipse(x2, y2, size2, size2);
push();
fill(255);
ellipse(x2 - 2, y2, size2 - (size2*0.6), size2 - (size2*0.6));
pop();
var x3 = (dist(mouseX, mouseY, width/2, height/2));
var y3 = (dist(mouseX, mouseY, width/2, height/2)) * -1;
var size3 = dist(mouseX, mouseY, width/2, height/2)/5;
ellipse(x3, y3, size3, size3);
push();
fill(255);
ellipse(x3 - 2, y3, size3 - (size3*0.6), size3 - (size3*0.6));
pop();
var x4 = width/2;
var y4 = (dist(mouseX, mouseY, width/2, height/2)) * -1.5;
var size4 = dist(mouseX, mouseY, width/2, height/2)/5;
ellipse(x4 - 200, y4, size4, size4);
push();
fill(255);
ellipse(x4 - 200, y4, size4 - (size4*0.6), size4 - (size4*0.6));
pop();
var x5 = width/2;
var y5 = (dist(mouseX, mouseY, width/2, height/2)) * 1.5;
var size5 = dist(mouseX, mouseY, width/2, height/2)/5;
ellipse(x5 - 200, y5, size5, size5);
push();
fill(255);
ellipse(x5 - 200, y5, size5 - (size5*0.6), size5 - (size5*0.6));
pop();
}
}


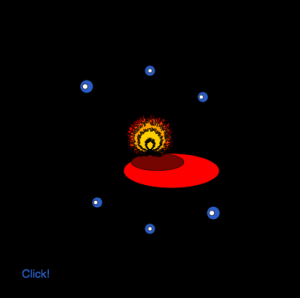
I liked working on this project because I gained a better understanding of how extensively you can use math in P5. I discovered how to make the flames by accident by randomizing one of the values in the equation of the curve. Once this happened, I was able to come up with a concept for the rest of the project. I liked working with colors and the mouseIsPressed conditional to change the image from red fire to blue fire. In the future, I would like to have a better ability to implement the map() function, as I feel that it would have been useful for my goals in this project.
![[OLD FALL 2018] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)