Category: Project-07-Curves

sketch

// Nadia Susanto
// Section B
// nsusanto@andrew.cmu.edu
// Project-07-Curves

var angle = 0;

function setup() {
    createCanvas(480, 480);
    background(220);
    angleMode(radians);
}

function draw() {
    //making the fill to be a combo of random colors
    var r = random(0, 100);
    var g = random(100, 150);
    var b = random(200, 275);
    frameRate(5);
    push();
    fill(r, g, b);
    translate(width/2, height/2); //drawn to be in the middle
    //rotating the asteroid
    angle += 1;
    rotate(angle);
    drawCurve(); //calling function
    pop();

}

function drawCurve() {
    var b = mouseY/2;
    var t = map(mouseY, 0, 200, 40, 120); //constraint

    //creating the astroid
    beginShape();
    for (var i = 0; i < 100; i++) {
      t = map(i, 0, 100, 0, TWO_PI);
      //reference from http://mathworld.wolfram.com/Astroid.html
      var x = 3 * b * cos(t) + b * cos(3 * t);
      var y = 3 * b * sin(t) - b * sin(3 * t);
      vertex(x, y);
    }
    endShape();


}

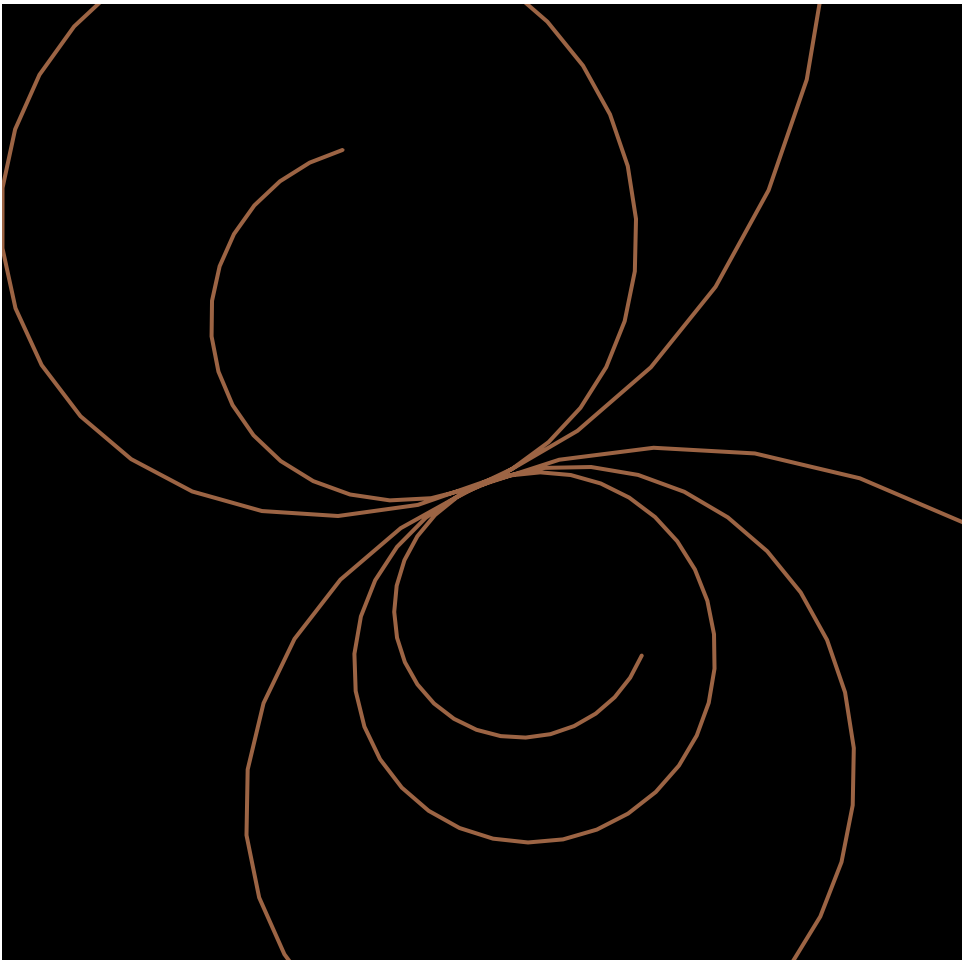
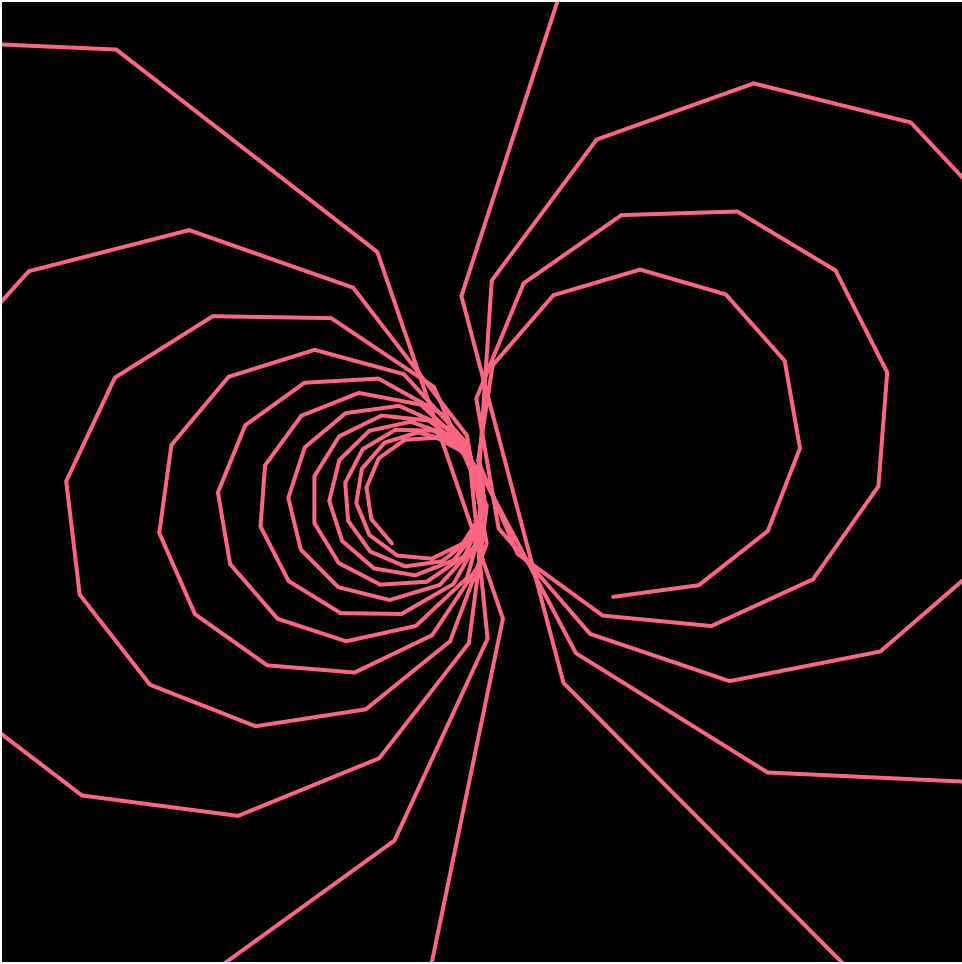
It was hard figuring out which curve to use as there were so many that were pretty, but I ended up choosing to go with the asteroid curve. I figured that a star-shaped curve could be beautiful especially when rotating. With the rotation it looks like a christmas tree star or it even looks flowerly-like. I also played around with the random colors and constrained it to be only blue/purple shades. I then used mouseX and mouse Y in order to determine the size of the asteroid. Overall, I am pretty happy with the result and it looks beautiful.

Trying to get the curve was pretty difficult. The website had a lot of equations on it and I picked through them to get the information I needed. Once I got the curve I wanted, the issue rose of how to implement it in the code. After experimenting for a bit and looking at the code given on the assignment instructions for reference, I eventually figured it out. After getting the curve to work, I changed some values so that it changed along with the mouse, making it interactive. I also added and changed other elements to make the image prettier, such as adding colors and flowers.

sketchsal

var num_points = 100;//number of points being drawn

function setup() {
    createCanvas(480, 480);
    frameRate(25);
}

function draw() {
    var hW = width / 2;//half of width
    var hH = height / 2;//half of height
    background("pink");
    for(var i = 0; i < 3; i++){//draws rows of elements
        for(var g = 0; g < 3; g++){//drawns columns of elements
        ellipse((width / 2) * i,(height / 2) * g, (mouseX / 4) * 1,
            (mouseX / 4) * 1);//circles being drawn
        }

    }
    //circles
    noStroke();
    fill(255, 232, 232);
    ellipse(120,120, 10,10);//upper left
    ellipse(360,120, 10,10);//upper right
    ellipse(120,360, 10,10);//lower left
    ellipse(360,360, 10,10);//lower right
    //flowers
    fill(255, 69, 69);
    ellipse(120,120, 5,15);//upper left
    ellipse(360,120, 5,15);//upper right
    ellipse(120,360, 5,15);//lower left
    ellipse(360,360, 5,15);//lower right

    fill(255, 117, 117);
    ellipse(120,120, 15,5);//upper left
    ellipse(360,120, 15,5);//upper right
    ellipse(120,360, 15,5);//lower left
    ellipse(360,360, 15,5);//lower right
    fill('red');//makes circles red
    stroke(0);//makes everything outlined

    //draw curve (Astroid) 
    push();
    translate(width / 2, height / 2);//(240,240)
    drawAstroid();
    pop();
}
function drawAstroid() {//function that draws curve
    var x;//calls x
    var y;//calls y
    var vx = mouseX / 5.0;//value of mouseX divided by 5 
    fill(255, 200, 200);//pink
    beginShape();//makes it so that the lines don't stay after being drawn
    //(there isn't a bunch of overlapping blackness)
    for (var i = 0; i < num_points; i++) {//increments elements from 0 to 100
        var t = map(i, 0, num_points, 0, TWO_PI);//runs curve from 0 to 2 pi
        
        x = vx * pow(cos(t * vx),3);//formula for x values
        y = vx * pow(sin(t * vx),3);//formula for y values
        vertex(x, y);
    }
    endShape(CLOSE);//ends shape
}

reshin-project07

/*Rachel Shin
reshin@andrew.cmu.edu
15-104 Section B
Project 07- Composition with Curves
*/

var numPoints = 300;
var angle = 0;


function setup() {
    createCanvas(480, 480)
    r = random(255);
    g = random(255);
    b = random(255);
}    



function draw() {
    background(0);

    push();
    translate(width / 2, height / 2); //center on canvas
    drawHypotrochoid();
    pop();

    push();
    translate(mouseX, mouseY); //center of curve based on mouse position
    rotate(radians(angle)); //rotates on center point
    drawTrifolium();
    pop();

    angle = angle + 4; // speed of rotation
}  
  
function drawHypotrochoid() { //http://mathworld.wolfram.com/Hypotrochoid.html
    var x;
    var y;
    
    //map boundaries
    var h = map(mouseY, 0, height, 0, 200); //size changes based on mouseY
    var a = map(mouseX, 0, width, 0, 200); //size changes based on mouseX
    var b = a / 8;

    //Hypotrochoid curve
    beginShape();
    for (var i = 0; i < numPoints; i ++) {
        stroke(r, g, b);
        strokeWeight(2);
        noFill();
        var t = map(i, 0, 200, 0, TWO_PI)
        x = (a - b) * cos(t) + h * cos(((a - b) / b) * t)
        y = (a - b) * sin(t) - h * sin(((a - b) / b) * t)
        vertex (x, y)
    }
    endShape(CLOSE);
}


function drawTrifolium() { //http://mathworld.wolfram.com/ConicalSpiral.html    
    var x;
    var y;
    var r;

    //constrain    
    var a = constrain(mouseX, width / 5, width / 2);
    
    //outline of light blue spinning trifolium
    noFill();
    stroke(195, 217, 227);
    strokeWeight(0.5);

    //Trifolium curve
    beginShape();
    for (var i = 0; i < numPoints; i++) {
        var t = map(i, 0, numPoints, 0, TWO_PI);
        r = - a * cos(3 * t);
        x = r * cos(t);
        y = r * sin(t);
        vertex(x, y);
    }
    endShape(CLOSE);
}

This project took me a while because it took me a while to figure out how to compute each curves. Maneuvering it around the canvas was more interesting for me because it allowed me observe how the code I wrote computed it to animate a certain way.

sketch

//Minjae Jeong
//Section B
//minjaej@andrew.cmu.edu
//Project-07



function setup() {
    createCanvas(480, 480);
    background('black');
}

function draw() {
    push();// draw in the middle
    translate(width / 2, height / 2);
    drawHypotrochoid();
    pop();
}

//Equations from http://mathworld.wolfram.com/Hypotrochoid.html
 function drawHypotrochoid() {
    var x;
    var y;
    var a1 = mouseX; //move mouse to control hypotrochoids drawing
    var a2 = mouseY;
    var h = 5;

    beginShape(); //draw hypotrochoid
    for (i = 0; i < 480; i += 5){
        var t = map(i, 0, 200, 0, width);
        x = (a1- a2) * cos(t) + h * cos(t * (a1 - a2) / a2);
        y = (a1- a2) * sin(t) - h * sin(t * (a1 - a2) / a2);
        vertex(x, y);
    }
    endShape();



}

This simple looking black and white drawing with hypotrochoids attracted me more than other colorful tries in many reasons. First of all, the first impression is very wild, and simple. With the mouse cursor starting at the middle of the canvas (240, 240), the canvas starts black, and creates white spaces as the mouse moves. The fun part is, the background will never be pitch black once you move your mouse.

The mouse movement is sensitive, the drawing can change in many ways according to the user control. Although it can’t go full black unless refreshing the page, the drawing can go all-white which can reset the drawing.