// CJ Walsh
// Section D
// cjwalsh@andrew.cmu.edu
// Project 07
function setup() {
createCanvas(480, 480);
cx = width/2;
cy = height/2;
// list of colors for my larger lines
c1 = ['green', 'teal', 'cornflowerblue', 'royalblue', 'darkslateblue', 'navy'];
}
function draw() {
background("lightcyan");
h = cx;
w = cy;
s = PI/8;
noFill();
mx = constrain(mouseX, 0, cx);
my = constrain(mouseY, 0, cy);
// loop to establish all of the curves I draw
for (i = 0; i <= 2*PI; i+=s) {
// thin orchid lines
for (k = 0; k < 5; k++) {
push();
strokeWeight(1);
stroke('orchid');
translate(cx, cy);
rotate(i);
ellipse(mx - 30 - 10*k, my - 30 - 10*k, 120, 120);
pop();
}
// larger blue/green lines
for (j = 0; j < 12; j++) {
push();
strokeWeight(3);
stroke(c1[j%6]);
translate(cx, cy);
rotate(i);
ellipse(mx + 4*j, my + 4*j, 3*mouseX/2, 3*mouseY/2);
pop();
}
// small black dots
for (l = 0; l < 30; l++) {
push();
strokeWeight(2);
stroke('black');
translate(cx, cy);
rotate(i);
ellipse(mx - 60*l, my - 60*l, 5, 5);
pop();
}
}
}
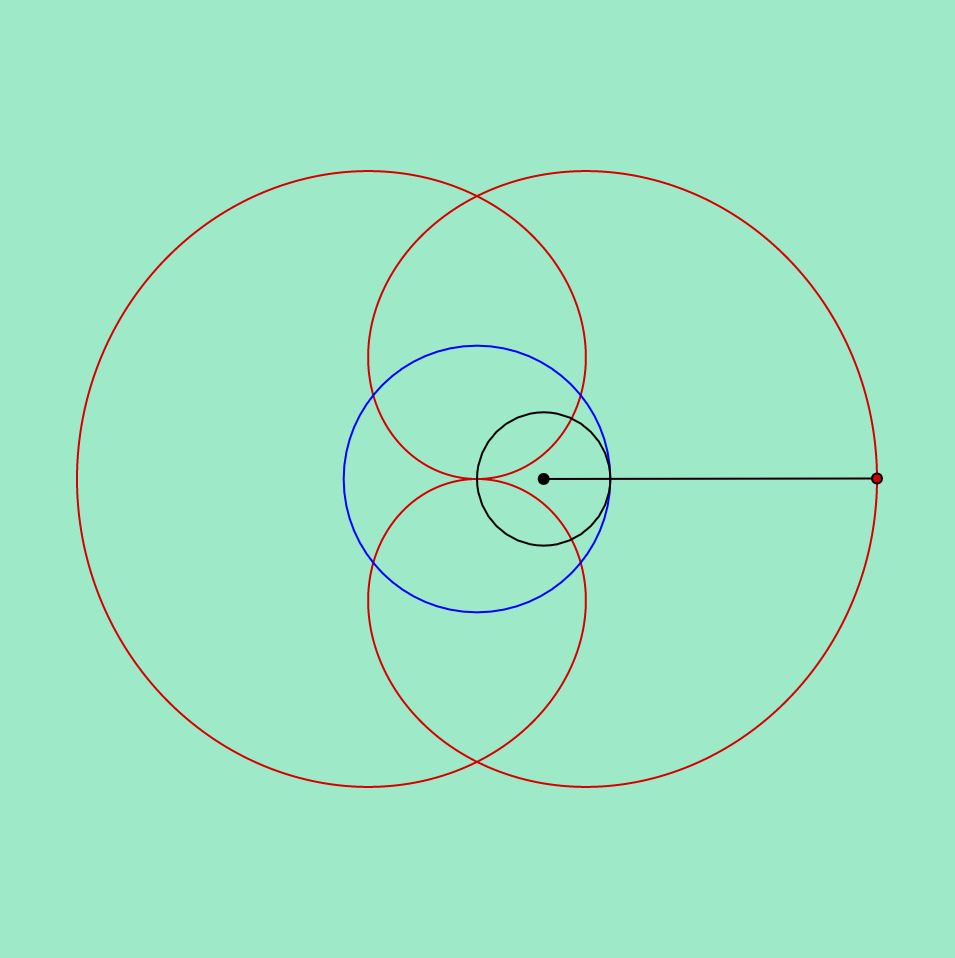
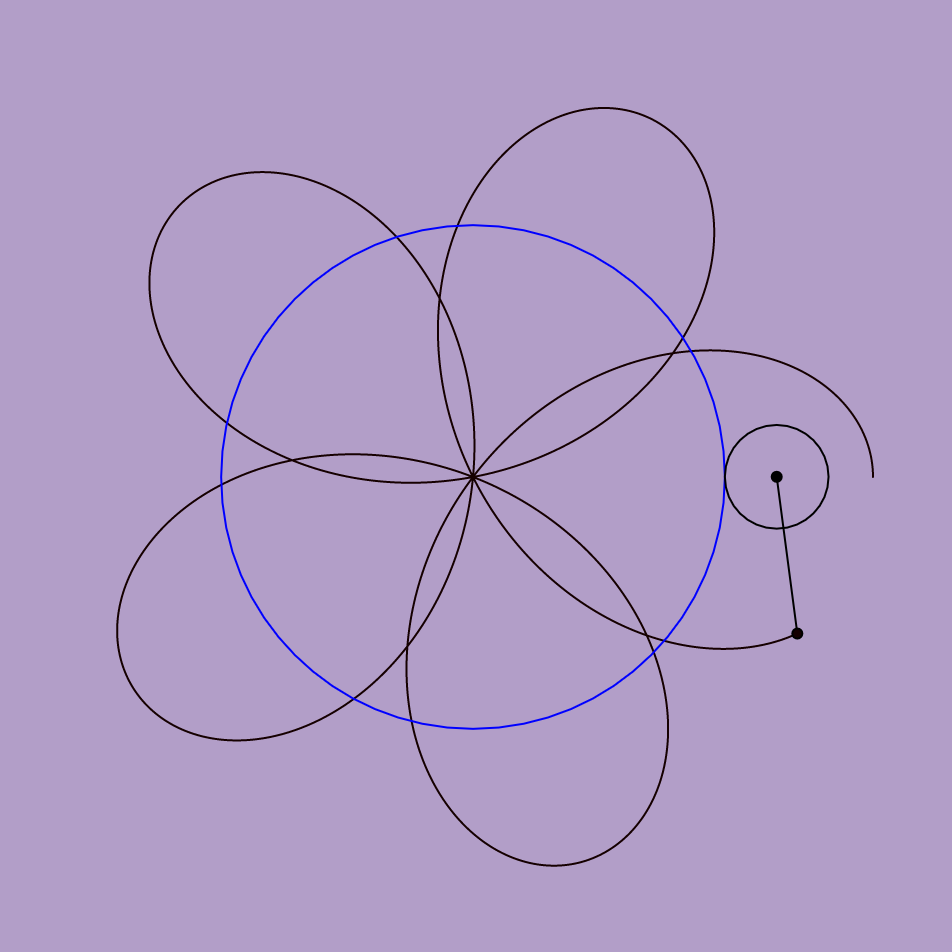
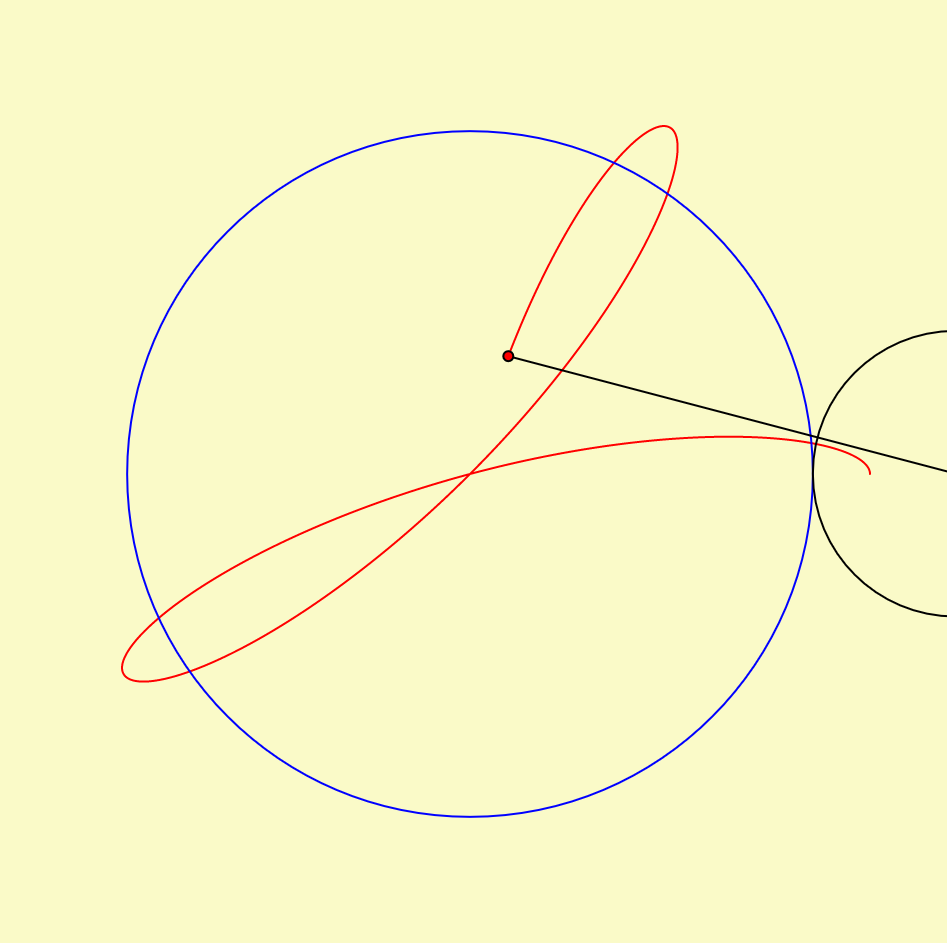
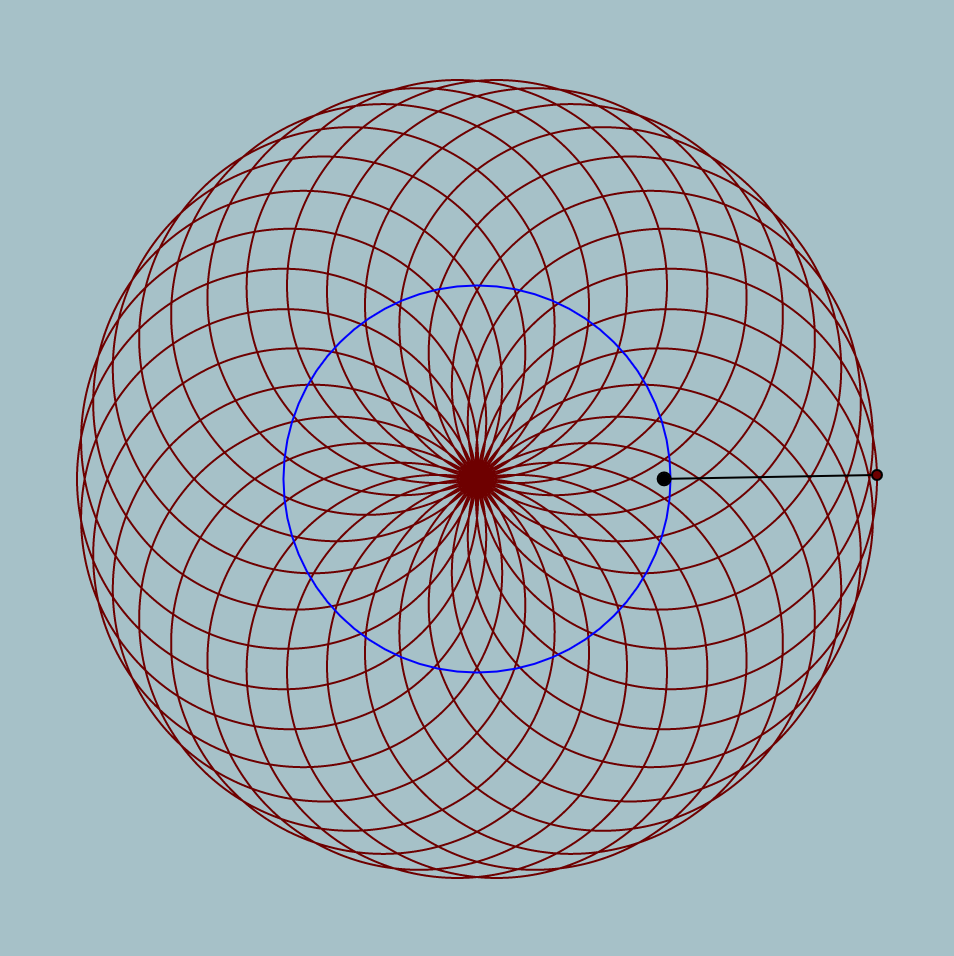
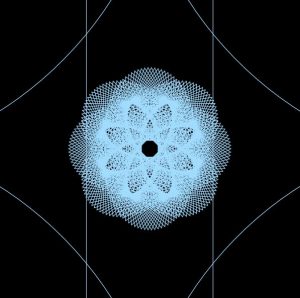
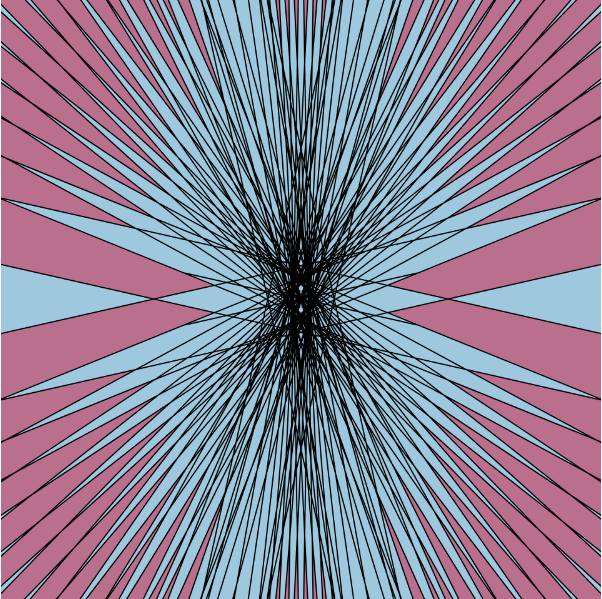
This was a super fun project to make in terms of experimenting with curves and loops. I started out by setting up an initial for loop and just drawing one curve. From there, I established some more loops to duplicate lines, or played around with some of the numbers so that I could create different shapes. This is another project that I could definitely see myself playing with or changing in the future because it was so fun to make. Below I included some of my favorite screenshots of the composition as it moves around.
![[OLD FALL 2019] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)