/*Katrina Hu
15104-C
kfh@andrew.emu.edu
Project-07*/
var nPoints = 100;
function setup() {
createCanvas(480, 480);
background(0);
}
function draw() {
push();
translate(width/2, height/2);
drawHypotrochoid();
drawAstroid();
pop();
}
function drawHypotrochoid() {
var x;
var y;
//mouse used to change color
var r = constrain(mouseX, 0, 255);
var g = constrain(mouseY, 0, 255);
var b = constrain(mouseY, 200, 255);
//stroke appearance
stroke(r, g, b);
strokeWeight(1);
noFill();
//hypotrochoid equation
var a = map(mouseX, 0, 600, 0, 300);
var b = 10
var h = map(mouseY, 0, 600, 2, 105);
beginShape();
for (var i = 0; i < nPoints; i++ ) {
var angle1 = map(i, 0, nPoints, 0, TWO_PI);
//equation of hypotrochoid
x = (a - b) * cos(angle1) + h * cos((a - b) * (angle1 / b));
y = (a - b) * sin(angle1) - h * sin((a - b) * (angle1 / b));
vertex(x, y);
}
endShape();
}
function drawAstroid() {
//mouse used to change color
var r = constrain(mouseX, 200, 255);
var g = constrain(255, mouseY/4, 50);
var b = constrain(mouseY, 200, 255);
//stroke appearance
stroke(r, g, b);
strokeWeight(2);
noFill();
//asteroid equation
var a = int(map(mouseX, 0, width, 4, 10));
var b = int(map(mouseX, 0, width, 0, 100));
beginShape();
for (var i = 0; i < nPoints; i++){
angle1 = map(i, 0, nPoints, 0, TWO_PI);
//equation of Astroid
x = (b / a) * ((a - 1) * cos(angle1) + cos((a - 1) * angle1));
y = (b / a) * ((a - 1) * sin(angle1) - sin((a - 1) * angle1));
vertex(x,y);
}
endShape();
}
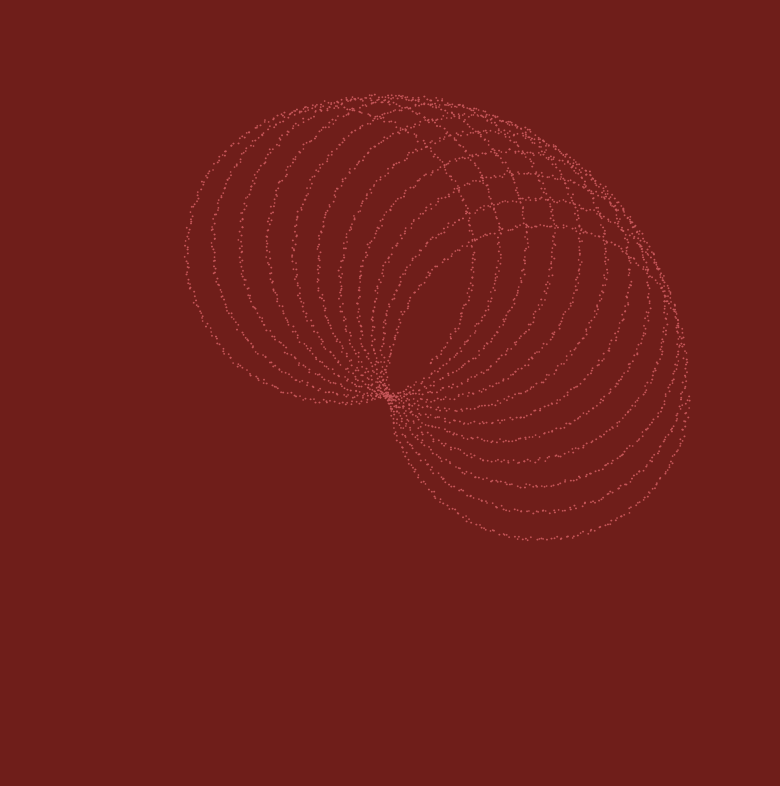
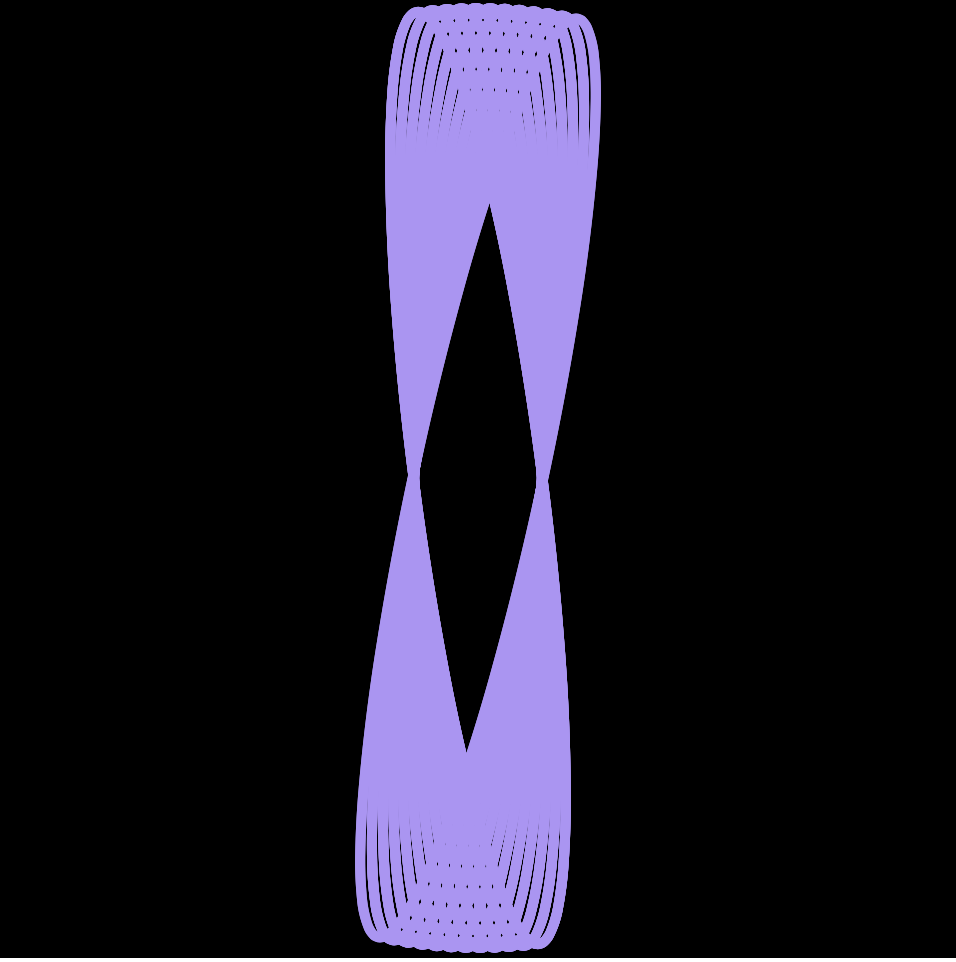
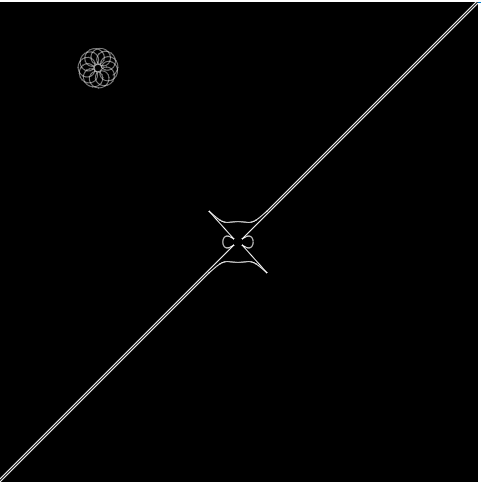
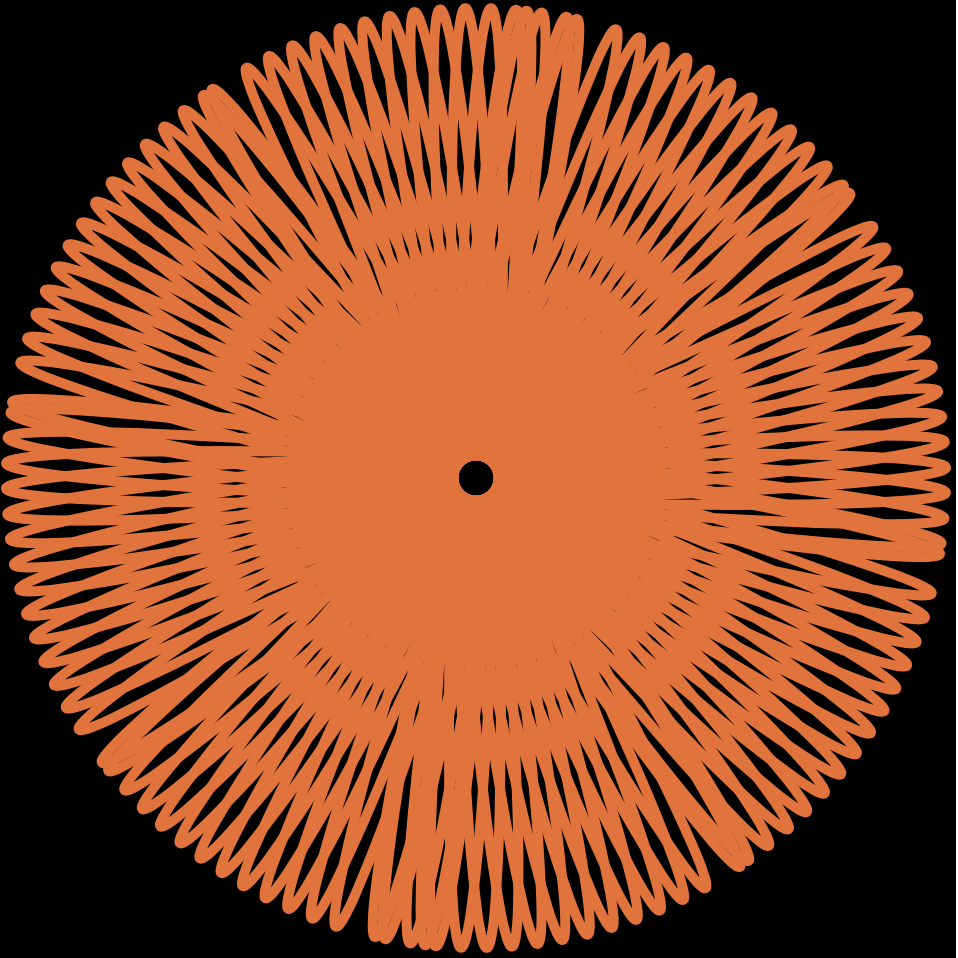
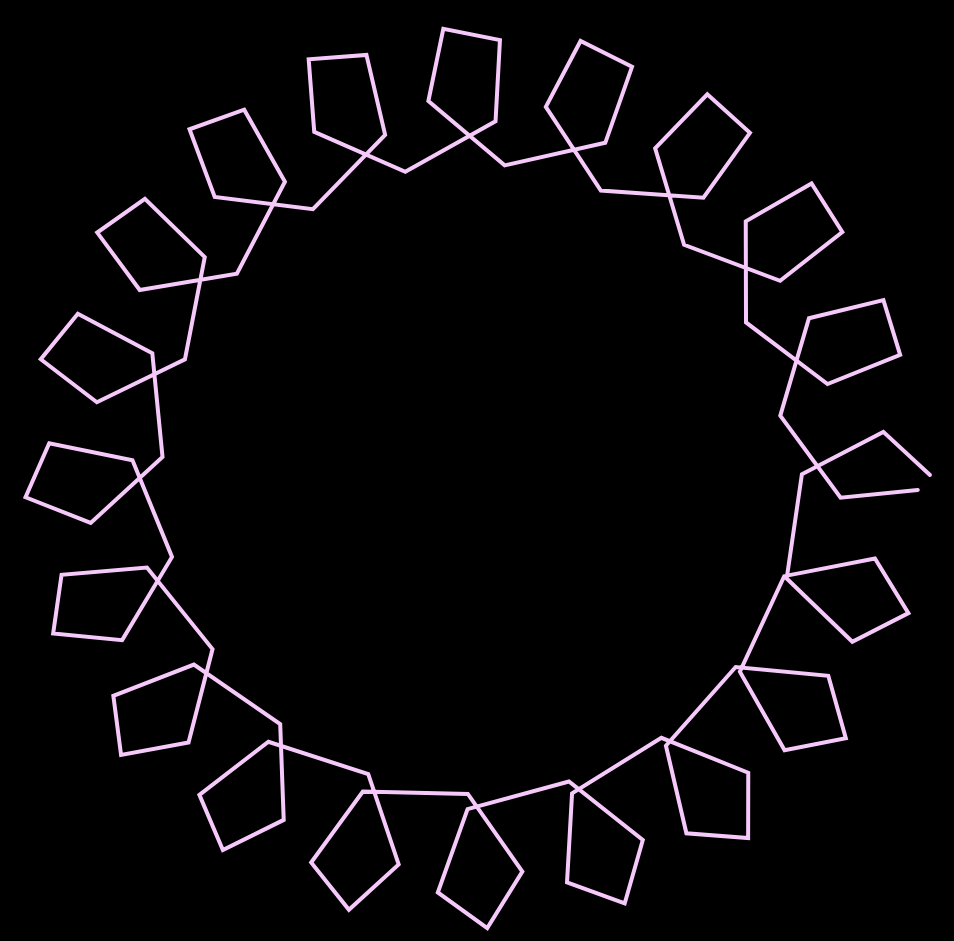
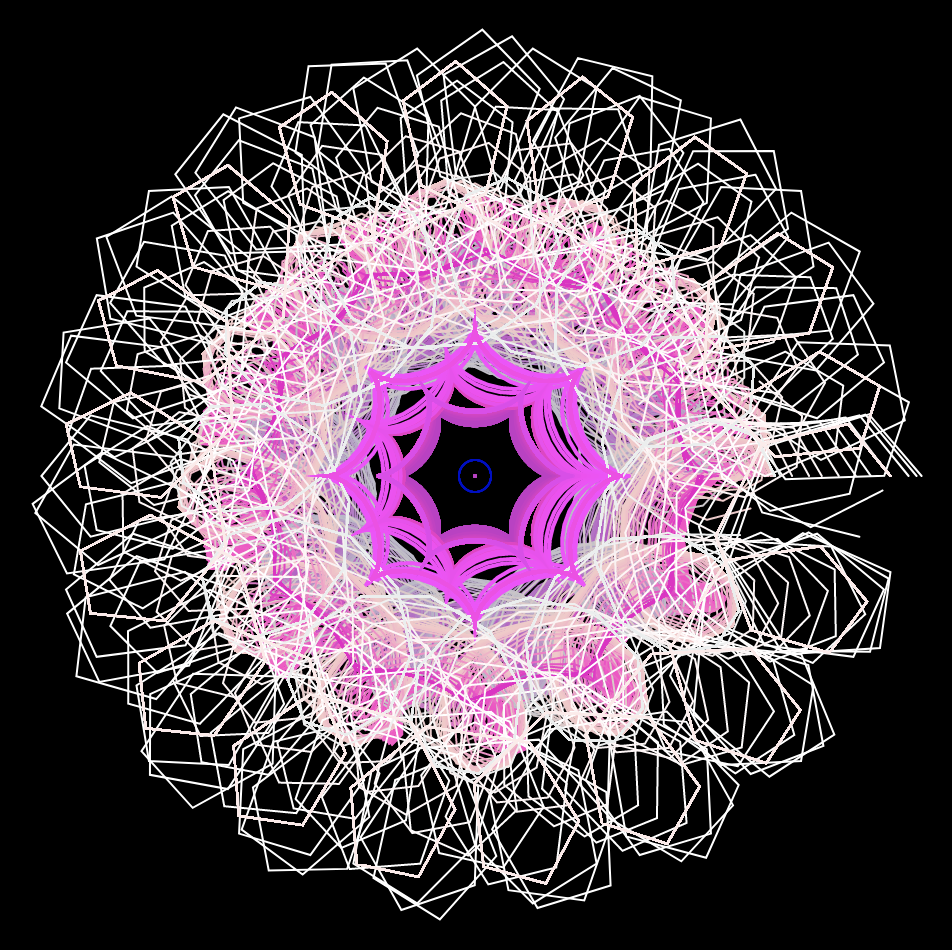
In my project I used a Hypotrochoid and an Asteroid. I decided to use my mouse to play around with the RGB values, which change depending on mouseX and mouseY. The project has a large Hypotrochoid on the outside with the Asteroid on the inside.
I decided to let it draw over itself, as it adds more curves when you move the mouse. I thought it added a cool layering effect where you could see all the colors on top of one another.
Overall, the project was fun to do as I learned a lot about experimenting with the different curves and parametric equations.
![[OLD FALL 2019] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)