Month: October 2016

The project I tried to create is made up of eight curves and parabola. The parameter a (the scale of the eight curves) and b (the scale of the parabolas) is controlled by the x coordinates of the mouse. The number and the rotation degree is controlled by the y coordinates of the mouse. When a user moves the mouse, he/she can expect a procedure of flower blossom or a comet with its long tail. I was intended to create a kaleidoscope through the intertwine and changes of different curves.
sketch

function  setup() {
  createCanvas(600, 600);
}
 
function draw(){
  background(200, 200, 255);
  //keep the size of the eight curve in a reasonable size
  var x = min(mouseX, width);
  //like the parameter to mouseX
  var a = map(x, 0, width, 0, 200);
  var b = map(mouseX, 0, width, 0, 400);
  //link the rotation to mouseY
  var deg = map(mouseY, 0, height, 0, 360);
  noFill();
  stroke(255);
  push();
  translate(width/2, height/2);
  for (var j = 0; j < deg; j += 3600/deg){
    rotate(720/deg);
    beginShape();
    curveVertex(0, 0);
    //draw the complete eight curve
    for (var i = -10; i < 10; i += 0.1){
         var x = a*sin(i);
         var y = a*sin(i)*cos(i);
         curveVertex(x, y);
    }
    curveVertex(0, 0);
    endShape();
    
    beginShape();
    curveVertex(0, 0);
    //draw the complate parabola curve
    for (var i = -10; i < 10; i += 0.1){
         var x = b*sq(i);
         var y = 2*b*i;
         curveVertex(x, y);
    }
    curveVertex(0, 0);
    endShape();
  }
  pop();
  

}

sketch

//Shannon Case
//Section D
//scase@andrew.cmu.edu
//assignment 07-A

var nPoints = 100;
//var valE = 2.718; // This is the value of # 'e'

function setup() {
    createCanvas(400, 400);
    frameRate(10);
}


function draw() {
   
    
    // draw the frame
    fill((mouseY/height)*100,(mouseY/height)*200,(mouseY/height)*255);
    rect(0, 0, width-1, height-1); 
    
    // draw the curve
    push();
    translate(width / 2, height / 2);
        drawEllipseEvoluteCurve();

    pop();

}

function drawEllipseEvoluteCurve() {
    // Ellipse Evolute
    // http://mathworld.wolfram.com/EllipseEvolute.html
    
    var x;
    var y;

    var a = constrain((mouseX / width), 0.1, 0.5);
    var b = constrain((mouseY / height), 0.1, 0.5);
    
    fill((mouseX/width)*255,(mouseX/width)*100,(mouseX/width)*255);
    strokeWeight(5);
    stroke((mouseX/width)*200,(mouseX/width)*55,(mouseX/width)*255);
    beginShape();
    for(var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);

        x = ((Math.pow(a+(mouseX/45), 2) - Math.pow(b, 2)) / a * (Math.pow(cos(t), 3)));
        y = ((Math.pow(b+(mouseY/48), 2) - Math.pow(a, 2)) / b * (Math.pow(sin(t), 3)));
        vertex(x, y);

    }
            endShape(CLOSE);

}


    

For this project I really struggled with choosing a curve that worked. I chose a bunch that weren’t really able to move well with both the x and y values, but eventually decided on the Ellipse Evolute because it was more easily able to stretch and shrink with my mouseX and mouseY. I chose to have the background color evolve with the mouseY values and the color of the shape change with the mouseX values.

Project 7-ach

//Alison Hoffman
//Section D
//achoffma@andrew.cmu.edu
//Project 7 - Curves 

var points = 1000; // number of points 
function setup() {
    createCanvas(420,420);
}

function draw() {
    background(7,26,85);
    push();   // medium curve
    translate(75,75);
    rotate(radians(230));
    drawCurve(85,4,200);
    pop();
    push();
    translate(width/6*5,height/3*2); // lightest
    rotate(radians(90));
    drawCurve(100,2,100);
    pop();
    push();
    translate(width/2,height/2-15); //thicker curve
    rotate(radians(65));
    drawCurve(30,8,60);
    drawCurve(45,8,60);
    pop();
}



function drawCurve(h,w,c) { //takes parameters, h (height variant), w(stroke Weight), and c (value of Green)
    var a = constrain(mouseY/5,0,height); // constrains a to mouseY
    var b = constrain(mouseX/15,0,width); // constrains mouseX to b
    var h = h; // variant degree of curve
    var x;
    var y;
    stroke(mouseX,c,mouseY); // color of stroke depends on input and mouse postions
    strokeWeight(w);
    //
    beginShape();
    noFill();
    for(var i = 0; i < points; i++){
        var t = map(i,0,points,0,TWO_PI); // maps theta to the size of the circle
        x = ((a+b)*cos(t))-(h*cos(((a+b)/b)*t)); // I reversed the signs of the orginal formula in order to invert the curve
        y = ((a+b)*sin(t))-(h*sin(((a+b)/b)*t)); // reversed signs to invert the curve
        curveVertex(-x,-y);
    }
    endShape();
}

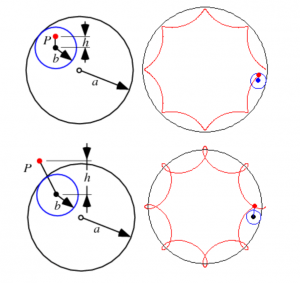
This project was really intimidating at first, but once I found a curve that I thought I could replicate it became easier to understand the math behind it. I chose to create a Epicycloid (pictured below). However, I didn’t really like how it created a flower like curve, so I inverted the signs of the formula (- to + and + to -) in order to have the ‘petals’ point inward. I also made the color of the curve depend on the position of the mouse and an input parameter. I chose to do multiple curves to show how the shape changed with varying stroke weight. Overall, once I got started and playing around, I actually ended up really enjoying this project.

Crystallize

I really enjoyed playing around with the equations and variables. During the course of my experimentation, I discovered a few cool effects combining different curves, but they all looked too chaotic. In the end, I chose this one, which is more simple and resembles an interesting crystallizing effect. It consists of an array of spiky shapes, which are modifications of a deltoid equation, that accumulate as the mouse moves across the canvas.

Sihan – crystallize

//Sihan Dong
//sihand@andrew.cmu.edu
//Section B
//Project Week 07: curves

var nPoints = 30;

function setup() {
    createCanvas(600, 400);
}

function draw() {
	background(255, map(mouseX, 0, width, 0, 200), map(mouseY, 0, height, 0, 200));
	stroke(255);
    noFill();
    drawDA();
}

function drawDA() {
	translate(width/2, height/2);
	var x = [];//array of spiky curves
	var y = [];
	var xa;//variables of circular curve
	var ya;
	
//only draw curves when mouse is within canvas
	if (mouseX < width & mouseY < height) {

    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        for(var j = 0; j < min(mouseX/50, width); j++) {
        	var a = map(mouseX, 0, width, 0, 150);
			var d = map(mouseY, 0, width, 5, 8*j);
		//spiky curve
        	x[j] = j*d*cos(t) + j*cos(j*t);
        	y[j] = j*d*sin(t) - j*sin(j*t);
    	//circular curve    
        	xa = a*cos(t);
        	ya = a*sin(t);

        	vertex(xa, ya);
        	vertex(x[j], y[j]);
    	}
    }
    endShape();
    print(d);
    print(mouseY);
	}
}