Category: Section C

sketch

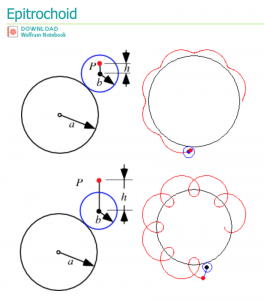
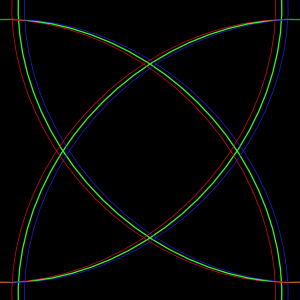
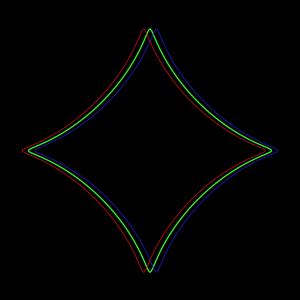
var x;
var y;

function setup() {
    createCanvas(480, 480);
    frameRate(25);
}

function draw() {
	background(0, 0, 0, 57);
	noFill();
	drawDeltoid();
	drawDeltoid2();
	drawDeltoid3();
}

// Outermost circle
function drawDeltoid(){

    var nPoints = 50;
	var radius = 50;
	var separation = 60;
	strokeWeight(1);
	stroke(150, 205, 255);
    push();
    translate(4 * separation, height / 2);
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var range = map(mouseX, 0, width, 0, 200)
        var px = range * cos(i) + cos(2 * i);
        var py = range * sin(i) - sin(2 * i);
        vertex(px + random(-mouseX / 30, mouseX / 80), py + random(-mouseX / 30, mouseX / 80));
    }
    endShape(CLOSE);
    pop();
}

// Middle circle
function drawDeltoid2(){

    var nPoints = 50;
    var radius = 50;
    var separation = 60;
    push();
    translate(4 * separation, height / 2);
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var px = mouseX / 4 * cos(i + mouseY / 50) + cos(2 * i);
        var py = mouseX / 4 * sin(i) - sin(2 * i);
        vertex(px + random(-5, 5), py + random(-5, 5));
    }
    endShape(CLOSE);
    pop();
}

// Inner circle

function drawDeltoid3(){

	var nPoints = 50;
    var radius = 50;
    var separation = 60;
    
    push();
    translate(4 * separation, height / 2);
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var px = mouseX / 4 * cos(i + mouseY / 50) + cos(2 * i);
        var py = mouseX / 4 * cos(i) - sin(2 * i);
        vertex(py + random(-5, 5), px + random(-5, 5));
    }
    endShape(CLOSE);
    pop();

}

At first I was a bit overwhelmed by all the mathematical equations for different curves, but once I settled on one and started playing around with it everything made a lot more sense. I really enjoyed the process of this project and changing every value in the equations to see and understand what they did.

sketch
Pretty early on I went through the site of curves, and I found the heart curves and decided I anted to do one. Conveniently, the one I thought looked best was straightforward to make. I was interested if JavaScript would take unicode as strings, and fortunately it does. Unfortunately, it’s plagued by an issue shared with many unicode sets – emoji. I had to make sure the unicode I wanted wouldn’t render as an emoji, because that just doesn’t look as crisp. In hindsight, it ould have been cool if I had used the function to generate a path for a moving heart like Lab 6, but there’s time for that in the future.

// Kevin Thies
// kthies@andrew.cmu.edu
// Section C
// Project 07 - Curve Composition

var pointNum = 100; // number of points in the heart
var bigScale = 20; // scale value of the largest heart
var smallScale = 2; // scale step of the iterations
var rotAngle = 1; // rotation angle of hearts
var rotIncrement = .02; // increment of rotation per frame in radians
var xScale; // mouse X - dependant scaling value of heart
var yScale; // mouse y - dependant scaling v alue of heart
var iterations = 10; // number of hearts drawn


function setup() {
  createCanvas(480,480);
}



function draw() {
    // style
    background(211,141,196);
    stroke(255,155,233);
    fill(0);

    // constrain the scaling of the X and Y of hearts
    xScale = constrain(map(mouseX, 0, width, 0, 1), .2, 1);
    yScale = constrain(map(mouseY, 0, height, 0, 1), .2, 1);

    // increment rotation
    rotAngle = rotAngle += rotIncrement;

    push();
    // move hearts to center of canvas
    translate(width/2, height/2);
    // rotate around center of canvas by the rotation angle
    rotate(rotAngle);

    // draw heart iterations
    for(var i = 0; i < iterations; i++) {
        // sizes decrease based on iteration number
        textSize(2 * (iterations - i));
        strokeWeight(.2 * (iterations - i));
        heartPoints(bigScale - i * smallScale, xScale, yScale);
    }
    pop();
}



function heartPoints(s, xS, yS) {
    // from http://mathworld.wolfram.com/HeartCurve.html
    // x = 16sin^3(t)
    // y = 13cos(t) - 5cos(2t) - 2cos(3t)- cos(4t)
    var x;
    var y;

    // grab x and y coords for pointNum amount of points
    for(var j = 0; j < pointNum; j++) {
        var t = map(j, 0, pointNum, 0, TWO_PI);

        // calculate x and y of asterisks
        x = xS * s * (16 * pow(sin(t), 3));
        y = yS * s * (13 * cos(t) - 5 * cos(2 * t) - 2 * cos(3 * t) - cos(4 * t));

        // place a unicode heart at the point, counter-rotate it
        push();
        translate(x, y);
        rotate(-rotAngle);
        text("♥", 0, 0);
        pop();
    }
}

curves

// Justin Yook
// jyook@andrew.cmu.edu
// Section C
// Project 07

var nPoints = 250; // number of points drawn to create shape

function setup() {
    createCanvas(480, 480);
}

function draw() {
    background(0);
    fill(255);
    text("Modified Quadrifolum", 20, 40);

    // draw the curve
    push();
    translate(width / 2, height / 2);
    drawQuadrifoliumMod();
    pop();
}

function drawQuadrifoliumMod() {
    // http://mathworld.wolfram.com/Quadrifolium.html
    // Polar equation is in form: r = a * sin(2 * theta), but I modified 2 to 6 to create a flower

    var x;
    var y;
    var r;
    var a = constrain(mouseX, 60, 220);

    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var theta = map(i, 0, nPoints, 0, TWO_PI);

        // Modified Quadrifolium
        if (mouseX > width / 2) {
        fill(0, 191, 255);
        r = a * sin(6 * theta);
        x = r * cos(theta);
        y = r * sin(theta);
        vertex(x + random(-2, 2), y + random(-2, 2));
        }

        // Original Quadrifolium
        if (mouseX < width / 2) {
        fill(0, 191, 255);
        r = a * sin(3 * theta);
        x = r * cos(theta);
        y = r * sin(theta);
        vertex(x + random(-2, 2), y + random(-2, 2));
        }
    }
    endShape(CLOSE);
}

In this project, I used modified versions of the quadrifolium to create flower-like shapes. I was inspired by the way fire appears on gas stoves, so I made the shapes jiggle slightly. The parameter that is interactive is the size of the curves, and the number of flower petals. When the mouse moves to the right, more petals show up, and the size increases. When the mouse moves to the left, fewer petals show up, and the size decreases.

(click to reset.)

/* Hannah Cai
Section C
hycai@andrew.cmu.edu
Project-07-Curves
*/


var ra = 50; //radius of base circle
var rb = 10; //radius of revolving perimeter circle
var h = 0; //height of curve from the center of rb
var t; //time
var o; //opacity of background
var x;
var y;
var v; //velocity


function setup() {
    createCanvas(480,480);
    background(0);
    stroke(255);
    strokeWeight(1);
    frameRate(30); //.5x animation
}

function draw() {
    o = map(mouseY, 0, height, 100, 25); //maps mouseY to background opacity
    mouseY = constrain(mouseY, 0, height); //constrains mouseY to canvas
    background(0, o);
    v = map(mouseX, 0, width, 1, -1); //maps velocity of ra and h to mouseX 
    ra += v; 
    h += v;

    for (t = 0; t < TWO_PI; t += .01) { 
        push();
        translate(width / 2, height / 2); //moves origin to center
        //epitrochoid equation
        x = (ra + rb) * cos(t) - h * cos(((ra + rb) / rb) * t); 
        y = (ra + rb) * sin(t) - h * sin(((ra + rb) / rb) * t);
        point(x, y); //draws points on the curve
        pop();
    }
}

//resets animation when mouse is clicked
function mouseClicked() {
    ra = 50;
    h = 0;
    t = 0;
}

For my project, I chose the epitrochoid:

When writing the code for it, I felt more interested by the particle patterns formed by the curve rather than the curve itself, so I chose to focus on those. While I didn’t enjoy the math involved (there were some really interesting/beautiful curves that I wanted to try creating, but just couldn’t understand), I do think it’s cool that you can basically plug equations straight into code and generate visual effects with them. Overall, I enjoyed the project.

rjpark_curves

var nPoints = 300;
var angle = 0;

function setup() {
    createCanvas(480, 480);
}

function draw() {
    background(175, 110, 235); // resets background every time draw is called so only one curve shows

    push();
    translate(mouseX, mouseY); // center of curve follows mouse
    rotate(radians(angle)); // rotates on center of curve
    drawEightCurve(); // draws curve
    pop();

    angle = angle + 3.5; // speed of rotation
}

// http://mathworld.wolfram.com/ConicalSpiral.html    
function drawEightCurve() {
    var x;
    var y;
    var r;
    
    var a = constrain(mouseX, width / 6, width / 2.2);
    
    fill(60, 20, 35);
    stroke(160, 15, 90);
    strokeWeight(5);

    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        r = - a * cos(3 * t);
        x = r * cos(t);
        y = r * sin(t);
        vertex(x, y);
    }
    endShape(CLOSE);
}

I first went to the Mathworld curves site and found the trifolium curve. It reminded me of a fidget spinner and so I got inspired to create one using this curve. As a result, I created a function (drawTrifolium()) that would draw the trifolium curve and, to do this, I used the polar equation from the site. Within the function, I made the “a” variable dependent on my mouseX movement. This changes the size of the fidget spinner as mouseX decreases or increases. Then, within the draw() function, I called drawTrifolium() and translated it so that the center of the fidget spinner would be wherever my mouse (mouseX and mouseY) is. Below are two pictures of the minimum and maximum size of the fidget spinner.

catherine curves

// Catherine Coyle
// ccoyle@andrew.cmu.edu
// Section C
// Project 7  - Curves

// equations taken from http://mathworld.wolfram.com/Hypotrochoid.html

var n = 1;
var h = 2;
var t = 1;
var a;
var b;

function setup() {
    createCanvas(480,480);
}

function draw() {
    background(226, 237, 255);
    // number of 'rotations' is dependent on y
    n = map(mouseY, 0, height, .9, 1.1);
    // size of rotation circles is dependent on x
    h = map(mouseX, 0, width, 2, 4);
    // smaller helper functions below here
    a = aCalc();
    b = bCalc();
    drawHypotochroidShadow(t, a, b);
    drawHypotochroid(t, a, b);
}

// i broke a lot of the heavy math parts into smaller functions
// to make it more manageable
function aCalc() {
    return(2 * n * h / (n + 1));
}

function bCalc() {
    return(((n - 1) * h) / (n + 1));
}

function xPar(t, a, b) {
    var answer = (a - b) * cos(radians(t));
    var cosVal = ((a - b) / b) * t;
    answer = answer + h * cos(radians(cosVal));
    return answer;
}

function yPar(t, a, b) {
    var answer = (a - b) * sin(radians(t));
    var cosVal = ((a - b) / b) * t;
    answer = answer + h * sin(radians(cosVal));
    return answer
}

function drawHypotochroid(t, a, b) {
    stroke(193, 124, 124);
    noFill();
    // loops through entire curve and plot every point
    beginShape();
    for(var i = 0; i < width; i++){
        var x = map(xPar(i, a, b), -4, 4, 0, width);
        var y = map(yPar(i, a, b), -4, 4, 0, height);
        curveVertex(x, y);
    }
    endShape();
}

// same as above but with some offset just to look cool
function drawHypotochroidShadow(t, a, b) {
    stroke(66, 134, 244, 50);
    noFill();
    // loops through entire curve and plot every point
    beginShape();
    for(var i = 0; i < width; i++){
        var x = map(xPar(i, a, b), -4, 4, 0, width);
        var y = map(yPar(i, a, b), -4, 4, 0, height);
        curveVertex(x-4, y-4);
    }
    endShape();
}

This project was kind of hard to get started with but once I wrapped my head around it I found it very cool.

I probably spent a good hour on the mathworld website trying to settle on a curve, but found that a lot of them were too hard to implement. I decided to go with the hypotrochoid shape found here.

If you keep your mouse on the left end of the screen, the curve should stay within the canvas if you want to see an entire design. Otherwise, moving your mouse to the right will kind of ‘zoom in’ to the center of the curve.

It took a lot of experimenting and trial and error to make the program work right, but in the end it produced some nice results.

 

sketch

// Sophia S Kim
// Section C 1:30
// sophiaki@andrew.cmu.edu 
// Project-07-Composition with Curves

var nPoints = 200; 

function setup() {
  createCanvas(480, 480);
}

function draw() {
  background(0);
  
  //middle green diamond 
  push();
  translate(width/2, height/2);
  noFill();
  strokeWeight(2);
  stroke(35, 255, 0);
  drawAstroid();
  pop();

  //right blue diamond
  push();
  translate((width/2) + 10, height/2);
  noFill()
  stroke(35, 0, 255);
  drawAstroid();
  pop();

  //left red diamond
  push();
  translate((width/2) - 10, height/2);
  noFill()
  stroke(255, 0, 0);
  drawAstroid();
  pop();
}

  //atroid move based on mouseX and mouseY 
  // Asteroid - http://mathworld.wolfram.com/Astroid.html
function drawAstroid() {
  var x; //xvalue for astroid curve
  var y; //yvalue for astroid curve
  var a; //for mouse X movement 
  var b; //constrains mouseY values 0 to 300

  a = mouseX; 
  b = constrain(mouseY, 0, 300);

  beginShape(); 
  for(var i = 0; i < nPoints; i++) {
    var t = map(i, 0, nPoints, 0, TWO_PI);
    //for degrees based on i 

    x = 3 * a * (cos(t)) + b * (cos(3*t)); 
    y = 3 * a * (sin(t)) - b * (sin(3*t));
    vertex(x,y);
  } 
  endShape();
}

For the “Composition with Curves,” I decided to do an “Astroid” curve, which is a 4-cusped hypocycloid. At first, I was really confused which equation I use for the parametric equations, because the website offered 3 equations for each variable (x, y). I tried all three for each variable to see which one showed the diamond-like shaped curves. Within that process, I got static-like lines, which looked beautiful but was not what I wanted in my final product. After many trials and the right equations, I was able to find the diamond-like curves and create 3 different copies with different colors using push() and pop(). I really liked the way my code turned out, because the changes of the curves reminded me of the Louis Vuitton branding.