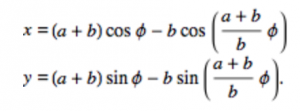// Jackie Chou
// Section E
// jwchou@andrew.cmu.edu
// Project-07-Curves
function setup() {
createCanvas(480, 480);
frameRate(60);
angleMode(DEGREES); //change angle mode
}
//goal: draw a flower with a center that pops up as the flower takes form
//then flower abstracts and center dissapears
function draw() {
background(200, 210, 253);
var R = map(mouseX, 0, width, 200, 255); //change stroke color of flower as mouseX changes
var G = map(mouseX, 0, width, 140, 250);
var B = map(mouseX, 0, width, 60, 130);
drawRanunculoiud(); //draw curve function
//flower center
translate(-width/2, - height/2); //move flower center to center
fill(170, 80, 130);
if (mouseX < 200 & mouseX > 50) { //draw flower center when flower starts to be visible
var ellipseSize = map(mouseX, 0, 200, 80, 0)
noStroke();
ellipse(width/2, height/2, ellipseSize, ellipseSize);
}
function drawRanunculoiud(){
beginShape();
noFill();
stroke(R, G, B);
translate(width/2, height/2); //move curve to center
for (var i = 0; i < width/5; i++){ //mouseX controls number of curves
constrain(mouseX/3, 100, 300); //constrain mouseX
var x;
var y;
var a = map(mouseX, 0, width, 30, 10);
var t = map(i, 0, mouseX, 10, 360);
//Ranunculoid http://mathworld.wolfram.com/Ranunculoid.html
x = a * (6 * cos(t) - cos(6 * t));
y = a * (6 * sin(t) - sin(6 * t));
vertex(x, y);
endShape();
}
}
}For this project, I had a bit of a hard time implementing the equation. However, looking and actually studying the diagrams on the site helped me understand what each variable affected the curve.
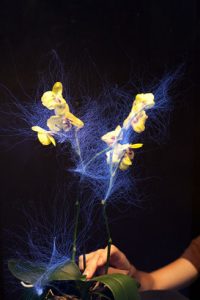
I eventually created a Ranunculoid, which looks like a flower with 5 pedals. When the mouse moves to the right, the flower grows but then eventually abstracts. When the form looks like a flower, a center disk forms. However, when the form abstracts, the center disk dissappears.
The first three frames showcase the growth of the flower.



The next three frames showcase the abstraction.



![[OLD FALL 2017] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)