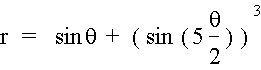Category: Project-07-Curves

sketch

//Yugyeong Lee
//Section B
//yugyeonl@andrew.cmu.edu
//Project-07

var nPointsA= 600;
var nPointsB= 200;
var nPointsC= 800;
var x;
var y;
var constrainX;

function setup() {
    createCanvas(480, 480);
}

function draw() {
	//ghosted background changing color based on mouseX
	var constrainX = constrain(mouseX, 0, width); //constraining mouseX in the page
	var r = map(constrainX, 0, width, 100, 39);
	var g = map(constrainX, 0, width, 43, 15);
	var b = map(constrainX, 0, width, 107, 54);
    background(r, g, b, 40);
    //Hypotrochoid & Ellipse
    push();
    translate(width/2, height/2);
    drawHypotrochoid();
    drawEllipse();
    pop();
    //Ranunculoid (only appears if mouseX is on left three quarter of page)
    if (constrainX < 3*width/4) {
   		push();
    	translate(width/2, height/2);
    	//mapping the angle of rotation based on mouseX
    	var angle = map(constrainX, 0, width, 0, 4 * TWO_PI);
		rotate(angle);
    	drawRanunculoid();
    	pop();
    }
}

function drawHypotrochoid() {
    constrainX = constrain(mouseX, 0, width); //constraining mouseX in the page
	var n = map(constrainX, 0, width, 0, .5);
    var a = 225;
    var b = n*a;
    var h = constrain(mouseY/2, 0, b);

    noFill();
    //change strokeWeight based on mouseX
    var s = map(constrainX, 0, width, .1, 2);
    //change stroke color based on mouseX
    var c = map(constrainX, 0, width, 255, 100);
    stroke(c)
    strokeWeight(s);
	beginShape()
		for (var i = 0; i < nPointsA; i++) {
			var t = map(i, 0, nPointsA, 0, 6*TWO_PI);
			x = (a - b)*cos(t) + h*cos((a - b)/b*t);
			y = (a-b)*sin(t) + h*sin((a-b)/b*t);
			vertex(x, y);
		}
	endShape(CLOSE);
 }

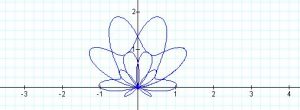
 function drawRanunculoid() {
    constrainX = constrain(mouseX, 0, width); //constraining mouseX in the page
    var a = 30;
    noStroke();
    //change fill oppacity based on mouseX
    var opacity = map(constrainX, 0, width, 10, 50);
    fill(255, 255, 255, opacity);
	beginShape()
		for (var i = 0; i < nPointsB; i++) {
			var t = map(i, 0, nPointsB, 0, TWO_PI);
			x = a*(6*cos(t)-cos(6*t));
			y = a*(6*sin(t)-sin(6*t));
        	ellipse(x, y, 5, 5); //ellipse at each points
		}
	endShape(CLOSE);
 }

function drawEllipse() {
    constrainX = constrain(mouseX, 0, width); //constraining mouseX in the page
    var a = 270;
    var b = 270;
    noFill();
	beginShape()
		for (var i = 0; i < nPointsC; i++) {
			var t = map(i, 0, nPointsC, 0, 6*TWO_PI);
			x = a*cos(t);
			y = b*sin(t);
			//ellipse at random position x and y range
        	ellipse(x+random(-50, 50), y+random(-50, 50), 3, 3);
		}
	endShape(CLOSE);
 }

I used three different curves for this interactive design: hypotrochoid, ranunculoid, and ellipse. The final product is interactive in that not only does the design react to position Y of the mouse location, the curves, the angle it rotates, stroke weight, stroke color, stroke opacity and background color all react to position X of the mouse location. Because of the circular movement of the other two curves, I wanted to create a “night-sky-with-blinking-stars” effect through creating an ellipse in which points are randomly positioned within a limited range with white blinking circles. The color palette was also chose to reflect the night sky atmosphere.

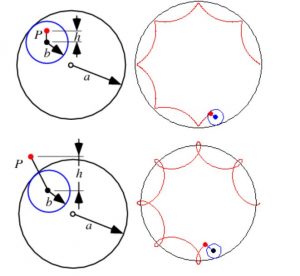
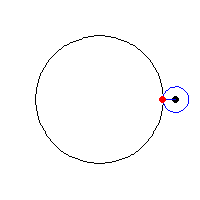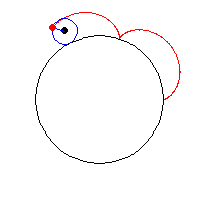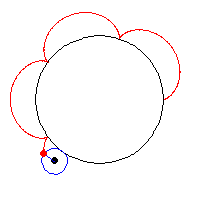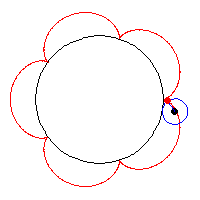
how Hypotrochoid & Ranunculoid works

sketch

//Selina Lee
//Section C
//selinal@andrew.cmu.edu
//Project-07

var nPoints = 70; //amount of elements
var Cissoid = 0; //http://mathworld.wolfram.com/CissoidofDiocles.html
var Conchoid = 0; //http://mathworld.wolfram.com/ConchoidofdeSluze.html

var titles = ["1. Cissoid", "2. Conchoid"];
var curveMode = Cissoid;

function setup() {
    createCanvas(480, 480);
    frameRate(10);
}

function draw() {
	background(255, 160, 60);  //orange background

	translate(240, 240); //place objects or focus on middle
	drawConchoidCurve(); //draw green and pink curves in back
	drawCissoidCurve(); //circles and blue lines in front
     
	
}

function drawCissoidCurve() {
	var x; //defining normal plane variables
	var y;

	var a1 = mouseX/20; //containing area of mouse interaction based on size or stretch of curves
	var a2 = mouseY/70;

	stroke(130, 130, 255); //blue lines
	strokeWeight(.5);
	beginShape(); //creating visuals based on Cissoid of Diocles curve
	for (var i = 0; i < nPoints; i++) {
		var t = map(i, 0, nPoints, 0, TWO_PI); //making i obtain to angle which is t 

		x = (10 * a1 * sq(t)) / (1 + sq(t)); //formulas for x and y of curve
		// 10 for x and 20 for y were used as constant values based on the composition attained in the index
		y = (20 * a2 * sq(t) * t) / (1 + sq(t));

		
		fill(250, 240, 220); //off white filling

		vertex(x, y); //draws single curve in normal direction for x and y on an index
		vertex(-x, y); //after adding this vertex, i noticed a greater variation and extension of the curves and lines so I continued this process
		vertex(x, -y);
		vertex(-x, -y);
		

		for(var ext = 0; ext < x; ext++) { //creating visuals deviating away from the lines but controlled by the same curve

			push(); //contain colors in this for loop not the colors also belonging to the blue line series
			fill(150, 255, 200); //green fill
			ellipse(ext * 10, -y * 5, 10, 10);  //greenish/aqua series of ellipses on top right and bottom left
			ellipse(-ext * 10, y * 5, 10, 10);

			fill(255, 120, 160); //reddish fill
			ellipse(ext * 15, -y * 19, 20, 20); //ellipses accompanying the ones in code written above
			ellipse(-ext * 15, y * 19, 20, 20);
	        pop();
		}

	}
	endShape(CLOSE);
}

function drawConchoidCurve() {
	var x2; //defining second x and y plane variables
	var y2;

	var b1 = mouseX; //containment of lines based on mouse interaction
	var b2 = mouseY;

	stroke(255, 100, 255); //magenta strokes
	strokeWeight(2); //thicker stroke
	beginShape();
	for (var j = 0; j < nPoints; j++) { 
		var ang = map(j, 0, nPoints, 0, TWO_PI); //setting the angle value same as var t in the first for loop for the Cissoid of Diocles curve

		x2 = ((1 / cos(ang)) + b1 * cos(ang)) * cos(ang); //formulas for Conchoid de Sluze curve	
        y2 = ((1 / cos(ang)) + b2 * cos(ang)) * sin(ang);

        fill(200, 255, 50); //lime green fill

        vertex(x2, y2); // this initial curve also only gave be one shape at first which looked like a flower petal from the center of the frame
        //this shape seemed more centered rather than side oriented like the Cissoid function so I experimented with on other vertex implementation focusing on the center of x
        vertex(-x2, y2); //created an inkblot array type of line series, more angular than round
        

        push(); // so that other functions not used before like noFill only affect these two vertex
        noFill(); //no fill so there is no overwhelming green
        vertex(x2 * 10, y2 * 10); //creating wider and bigger curve series of the same physical orientation and interaction
        vertex(-x2 * 10, y2 * 10);
        pop();
    }
    endShape(CLOSE);


}