Category: Project-07-Curves

circles

function setup() {
    createCanvas(480, 480);
}

function draw() {
    //mapping for colors lines and background
    var r = map(mouseX, 0, width, 0, 200);
    var g = map(mouseY, 0, height, 0, 255);
    var b = map(mouseX, 0, width, 0, 155);
    background(209, g, 100);
    stroke(r, 150, b);
    strokeWeight(3);

    //moving to middle of the canvas
    translate(width / 2, height / 2);
    noFill();
    drawHypotrochoid();
}

function drawHypotrochoid(){
    //variables to be used in the equation
    var x;
    var y;
    var h = width/2;
    var a = map(mouseX, 0, width, 0, PI);
    var b = map(mouseY, 0, height, 0, 1);

    //HYPOTROCHOID EQUATION
    // x = (a-b)*cos(angle) + h*cos(((a-b)/b) angle)
    // y = (a-b)*sin(angle) - h*sin(((a-b)/b) angle)

    beginShape();
        for(var i = 0; i < width; i+= 5){
            var angle = map(i, 0, width, 0, 360);
            x = (a - b) * cos(angle) + h * cos(((a-b)/b)*angle);
            y = (a - b) * sin(angle) - h * sin(((a-b)/b)*angle);
            vertex(x,y);
        }
    endShape();
}

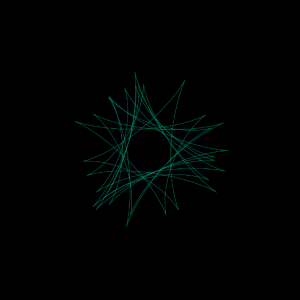
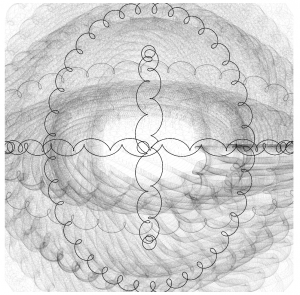
In order to fully understand the curves process, I tried to keep this project as simple as possible. This meant choosing a basic equation to start off with, which is how I ended up choosing the hypotrochoid curve. It took a little while to get used to how the rather long equation to generate the lines would semantically be converted into p5js; I had to add more multiplication stars than I had originally anticipated and had a lot of trouble trying to figure out that because when it wasn’t correct, nothing would render. I was able to play around with the numbers as well as colors by keeping this part of the project relatively simple. However, I am still mesmerized by the dancing lines from such a short amount of code.

Screenshots:

sketch

function setup() {
    createCanvas(400, 400);
    frameRate(10);
}


function draw() {
    background(226,236,236);
    
    strokeWeight(2);
    noFill();
    
    // draw the curve
    push();
    translate(width / 2, height / 2);

    // the curve inside
    for (var i = 0; i < 8; i++) {
        var r = 207-(207-152)/6*i;
        var g = 171-(171-92)/6*i;
        var b = 177-(177-103)/6*i;
        stroke(r,g,b);
        drawTetracuspidCurve();
        rotate(PI/14);
    }

    // the circle curve outside
    for (var i = 0; i < 6; i++){
        var r = 215-(215-147)/6*i;
        var g = 195-(195-126)/6*i;
        var b = 186-(186-118)/6*i;
        stroke(r,g,b);
        drawRanunculoidCurve();
        rotate(PI/3);
    } 
    pop();


}

function drawRanunculoidCurve() {
    var nPoints = 100;
    var x;
    var y; 
    var a = 100;
    var b = a / 5;   
    var ph = mouseX / 40;
    // control the shape in two opposite sides
    if (mouseY <height/2){
        var h = constrain(mouseY / 8, 0, b);
    } else {
        var h = constrain((height - mouseY) / 8, 0, b);
    }
    
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        // map the points onto angles
        var t = map(i, 0, nPoints, 0, TWO_PI);
        x = (a + b) * cos(t) - h * cos(ph + t * (a + b) / b);
        y = (a + b) * sin(t) - h * sin(ph + t * (a + b) / b);
        vertex(x, y);
    }
    endShape(CLOSE);    
}

function drawTetracuspidCurve(){
    var nPoints = 200;
    var x;
    var y;
    var a = 120;
    var ph = mouseX / 40;

    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        x = a / 4 * (3*cos(t) -  cos(ph + 3 * t));
        y = a / 4 * (3*sin(t) +  sin(ph + 3 * t));
        vertex(x, y);
    }
    endShape(CLOSE);    
}

Above are the process of my work. So, I combined two different kinds of curves in my project: Ranuncuidloid and Tetracuspid curves. The first shape is inspired from the form of flowers, and the other is inspired from the shape of a star. These two curves are all rotatable according to the x-coordinates of the mouse. Also, the flower shapes is generated from the y-coordinates of the mouse. The flower shape is more visible if the y-coordinates of your mouse is more towards the center, is like the flower is blooming. This project helps me understand more about the use of translate() and rotate(), which are my weakness. Also, I learned about many control elements in the curve equation, which is also meaningful.