Category: Uncategorized

Sarah Kang – Project 07 – Curves

curves

//sarah kang
//section c
//sarahk1@andrew.cmu.edu
//project-07-curves

 
 var ang = 0;
 var nPoints = 100; 

function setup() {
    createCanvas(480, 480);
}

function draw() {

    background(0);
    noFill();
    //orange curves
    push();
    translate(width / 2, height / 2);
    strokeWeight(2);
    stroke(255, 159, 28);
    drawHypo1();
    pop();
    //red curves
    push();
    translate(width / 2, height / 2);
    strokeWeight(8);
    stroke(181, 42, 74);
    drawHypo2();
    pop();
    //yellow curves
    push();
    strokeWeight(2);
    stroke(255, 240, 122);
    translate(width / 2, height / 2);
    rotate(radians(ang));
    ang += mouseX / 50;
    drawRan();
    pop();
}
//Ranunculoid Curve 
function drawRan(){ //http://mathworld.wolfram.com/Ranunculoid.html
    var sz = 10;
    //curve
    beginShape();
    for (var i = 0; i < nPoints; i += 0.1){
      var xr = sz * (6 * cos (i) - cos (6 * i));
      var yr = sz * (6 * sin (i) - sin (6 * i));
      vertex(xr, yr);
    }
    endShape();
}

//Hypotrochoid Curve 1
function drawHypo1() { //http://mathworld.wolfram.com/Hypotrochoid.html

    var x;
    var y;
    //controls 
    var h = map(mouseY, 0, height, 0, 80);
    var a = map(mouseX, 0, width, 0, 300);
    var b = a / 8;
    //curve
    beginShape();
    for (var i = 0; i < nPoints; i ++) {
        var t = map(i, 0, 100, 0, TWO_PI)
        x = (a - b) * cos(t) + h * cos(((a - b) / b) * t)
        y = (a - b) * sin(t) - h * sin(((a - b) / b) * t)
        vertex(x, y)
    };
    endShape();
}

//Hypotrochoid Curve 2
function drawHypo2() { //http://mathworld.wolfram.com/Hypotrochoid.html

    var x;
    var y;
    //controls 
    var h = map(mouseY, 0, height, 0, 80);
    var a = map(mouseX, 0, width, 0, 300);
    var b = a / 12;
    //curve
    beginShape();
    for (var i = 0; i < nPoints; i ++) {
        var t = map(i, 0, 100, 0, TWO_PI)
        x = (a - b) * cos(t) + h * cos(((a - b) / b) * t)
        y = (a - b) * sin(t) - h * sin(((a - b) / b) * t)
        vertex(x, y)
    };
    endShape();
}

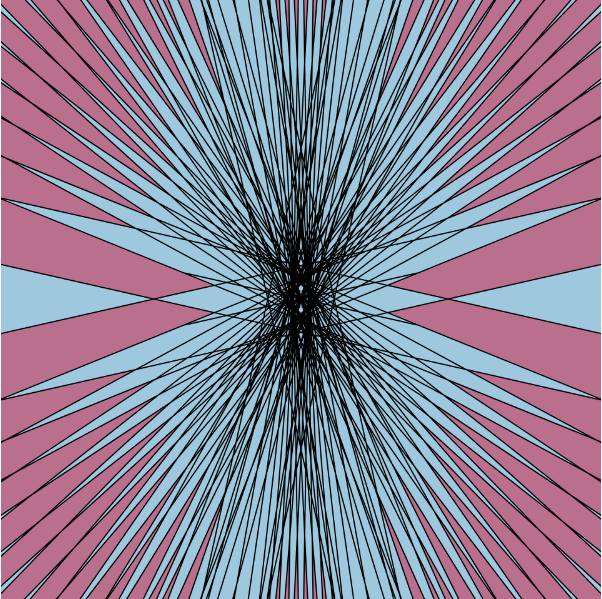
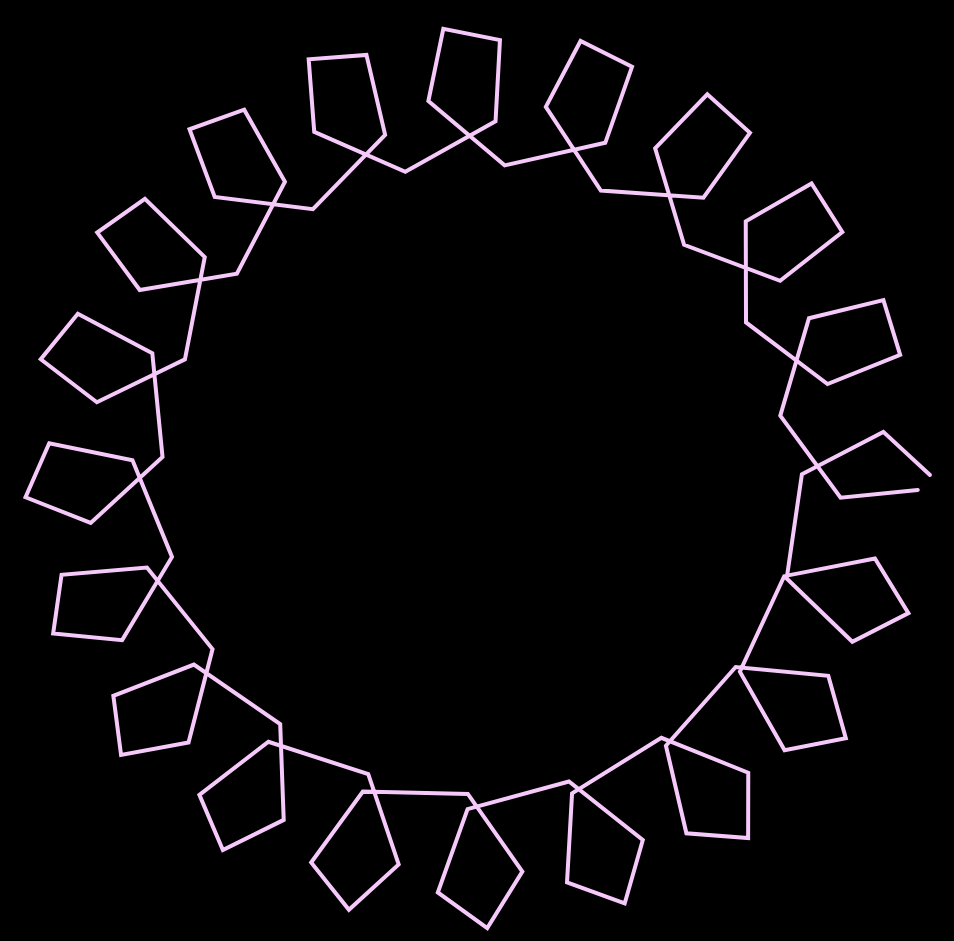
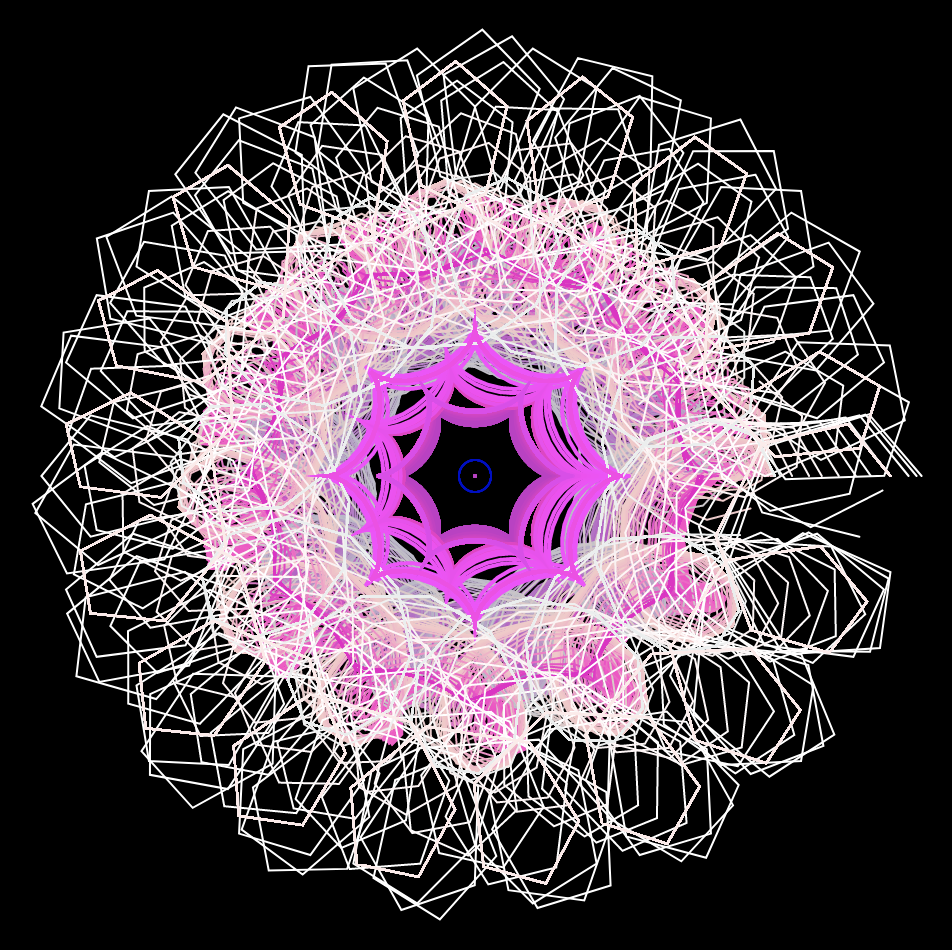
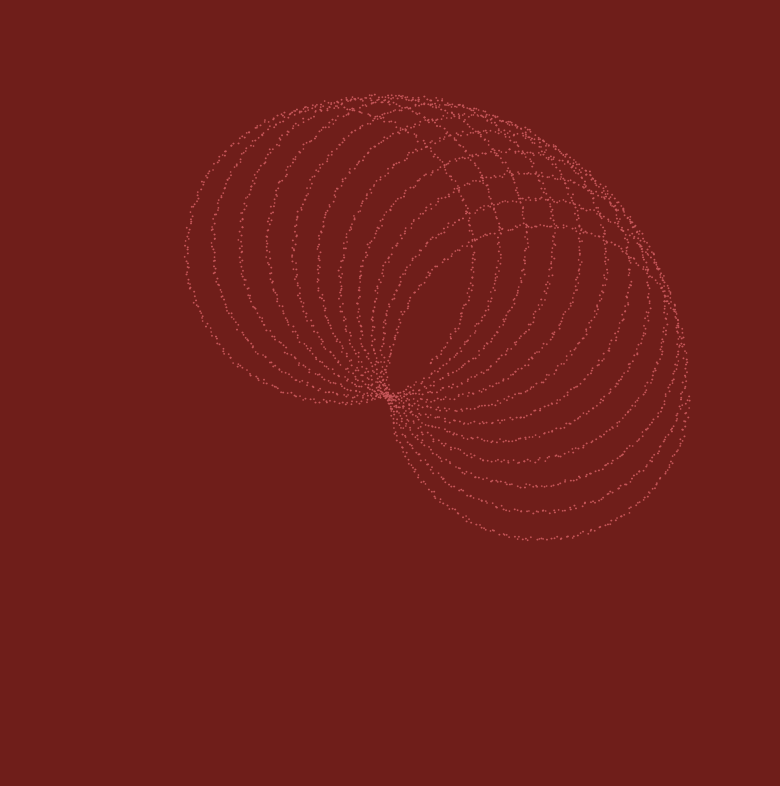
At first, trying to understand how the math equations were controlled was pretty confusing; after experimenting with the variables, I was able to adjust and change the outputs of the curves equations to how I wanted it to look. Then, I formatted the curves in terms of color and stroke weight to create a flowery design.

Carly Sacco – Project 07 – Curves

sketch

//Carly Sacco
//Section C
//csacco@andrew.cmu.edu
//Project 07 - Composition with Curves

var points = 200 //number of points
// for an episprial this will be sections
//the equation for an epispiral
//r = a sec (ntheta)
function setup() {
	createCanvas(480, 480);
}

function draw() {
	background(186, 112, 141);
	//calling the curve functions
	drawCraniodCurve1();
	drawCraniodCurve2();
}
	
function drawCraniodCurve1() {
var x;
var y;
var r;
var a = map(mouseX, 0, width, 0, width / 2); //makes the first epispiral relate to mouseX
var c = map(mouseY, 0, height, 0, height / 2); //makes the second epispiral relate to mouseY
var b = a / 5;
var p = 100;
var theta;

	//calling the curve functions to be drawn
	push();
	translate(width / 2, height / 2);
	fill(158, 200, 222); //blue
	beginShape();
	for (var i = 0; i < points; i += 1) {
		theta = map(i, 0, points, 0, TWO_PI);
		r = (a * (1 / cos((i + points) * theta))) //epispiral equation
		x = r * cos(theta);
		y = r * sin(theta);
		vertex(x, y);
	}
	endShape(CLOSE);
	pop();
}

function drawCraniodCurve2() {
	push();
	translate(width / 2, height / 2);
	fill(255, 77, 77); //red
	beginShape();
	for (var i = 0; i < points; i += 1) {
		var c = map(mouseY, 0, height, 0, height / 2);
		theta = map(i, 0, points, 0, TWO_PI);
		r = (c * (1 / cos((i + points) * theta))) //epispiral equation
		x = r * cos(theta);
		y = r * sin(theta);
		vertex(x, y);
	}
	endShape(CLOSE);
	pop();
}

For this project, I at first was trying to create an image more similar to a typical spirograph. However, after choosing to work with the epispiral, I liked how it almost looked like shattered glass. It reminded me of a comic strips and when an action was done there would be action bubbles. I then chose to animate it similarly to a “POW” action that could be drawn in the comics. Therefore, I overlayed the original epispiral with another with colors that could seem comic book like.

Katrina Hu – Project 07 – Curves

sketch_project07

/*Katrina Hu
15104-C
kfh@andrew.emu.edu
Project-07*/

var nPoints = 100;

function setup() {
    createCanvas(480, 480);
    background(0);
}

function draw() {
    push();
    translate(width/2, height/2);
    drawHypotrochoid();
    drawAstroid();
    pop();

}

function drawHypotrochoid() {
    var x;
    var y;
    //mouse used to change color
    var r = constrain(mouseX, 0, 255);
    var g = constrain(mouseY, 0, 255);
    var b = constrain(mouseY, 200, 255);
    //stroke appearance
    stroke(r, g, b);
    strokeWeight(1);
    noFill();
    //hypotrochoid equation
    var a = map(mouseX, 0, 600, 0, 300);
    var b = 10
    var h = map(mouseY, 0, 600, 2, 105);
    beginShape();
    for (var i = 0; i < nPoints; i++ ) {
        var angle1 = map(i, 0, nPoints, 0, TWO_PI);
        //equation of hypotrochoid
        x = (a - b) * cos(angle1) + h * cos((a - b) * (angle1 / b));
        y = (a - b) * sin(angle1) - h * sin((a - b) * (angle1 / b));
        vertex(x, y);
    }

  endShape();
}

function drawAstroid() {
    //mouse used to change color
    var r = constrain(mouseX, 200, 255);
    var g = constrain(255, mouseY/4, 50);
    var b = constrain(mouseY, 200, 255);
    //stroke appearance
    stroke(r, g, b);
    strokeWeight(2);
    noFill();
    //asteroid equation
    var a = int(map(mouseX, 0, width, 4, 10));
    var b = int(map(mouseX, 0, width, 0, 100));
    beginShape();
    for (var i = 0; i < nPoints; i++){
        angle1 = map(i, 0, nPoints, 0, TWO_PI);
        //equation of Astroid
        x = (b / a) * ((a - 1) * cos(angle1) + cos((a - 1) * angle1));
        y = (b / a) * ((a - 1) * sin(angle1) - sin((a - 1) * angle1));
        vertex(x,y);
    }
    endShape();

}

In my project I used a Hypotrochoid and an Asteroid. I decided to use my mouse to play around with the RGB values, which change depending on mouseX and mouseY. The project has a large Hypotrochoid on the outside with the Asteroid on the inside.

I decided to let it draw over itself, as it adds more curves when you move the mouse. I thought it added a cool layering effect where you could see all the colors on top of one another.

Overall, the project was fun to do as I learned a lot about experimenting with the different curves and parametric equations.

The starting Hypotrochoid curve
The curve layered over itself

ilona altman – project 07 – curves

sketch


// Ilona Altman
// Section A
// iea@andrew.cmu.edu
// Project-07

function setup() {
    createCanvas(400, 400);
    frameRate(10);
    noStroke();
}

function draw() {
//pink background
background(121,20,20);

// variables d/n = petal variations
var d = map(mouseX, 0, width, 0, 8);
var n = map(mouseY, 0, height, 0, 8);

// translating the matrix so circle is in the center
push();
translate(width/2, height/2);

//changing the colors
var colorR = map(mouseX, 0, width, 200,255);
var colorG = map(mouseY, 0, width, 50,245);
var colorB = map(mouseX, 0, width, 50,200);

// the loop generating the points along the rose equation
for (var i = 0; i < TWO_PI *3*d; i += 0.01) {
    var r = 150* cos(n * i);
    var x = r * cos(i);
    var y = r * sin(i);

    //making the circles more dynamic, and wobbly
    fill(colorR,colorG,colorB);
    circle(x +random(-1, 1), y + random(-1, 1), 1, 1);
    }

pop();
}

With this project, I was thinking a lot about auras, and energy, and how to make something digital that feels organic. I wanted to experiment with a flickery effect, achieved by alternating the size of the circles which compose this curve. I like the idea of these patterns looking like they are created from vibrations. I have been thinking about sacred geometry a lot, and about the patterns made in water when sound reverberates through it.

Shariq M. Shah – Looking Outwards 07 – Information Visualization

Aaron Koblin is an artist, designer, and programmer specializing in data and digital technologies and using computational techniques to visualize and develop information networks. One of his most compelling works focuses on visualizing flight pattern networks, which render paths of air traffic over North America through varieties of color and form. The FAA data for the flight networks was parsed through Processing and visualized to show nodes and overlaps among highly complex flight patterns. Another Intriguing work of Koblin’s, uses Amazon’s Mechanical Turk to spread out the work of developing an image of the hundred dollar bill across thousands of individuals to where each individual was unaware of the overall task. The computational process works in service of exploring the idea of an advancing economy and distribution of labor. These highly visual and creative ways of visualizing information by Aaron Koblin challenge conceptions of informational graphics and have the potential to become generative models for innovative thinking and development.

 

 

10, 000 Cents Image Produced through Mechanical Turk System
Flight Patterns Visualization 01
Flight Patterns Visualization 02
Home
Aaron Koblin’s Website

Shariq M. Shah – Project 07 – Curve

shariqs-a7-project

// Name: Shariq M. Shah
// Andrew ID: shariqs
// Section: C
// Project 07

//defining global variable for number of points

var nPoints = 500;


function setup() {
  createCanvas(400, 400);
}

function draw() {



  //stroke colors will be a function of mouseX location

  var r = map(mouseX, 0, width, 80, 250);
  var g = map(mouseY, 0, height, 80, 250);
  var b = map(mouseX, 0, width, 80, 250);


  //call drawEpitrochoidCurve function

  background(g, b * 2, r * 2);
  push();
  noFill();
  stroke(b, g, r);
  strokeWeight(0.5);
  translate(width/2, height/2);
  drawEpitrochoidCurve();
  rotate(radians(frameRate));
  pop();



  //call drawFermat function
  push();
  noFill();
  stroke(r, g, b);
  strokeWeight(0.5);
  translate(width/2, height/2);
  drawFermat();
  pop();

}


function drawEpitrochoidCurve() {

    // Epicycloid:
    // http://mathworld.wolfram.com/Epicycloid.html

    var x;
    var y;

    var a = map(mouseX, 0, width, 0, width/2);
    var b = a / 2;
    var h = height / 4;
    var ph = mouseX / 10;

    beginShape();
    for (var i = 0; i < nPoints; i++) {

        var t = map(i, 0, nPoints, 0, PI * 2);

       // defining curves as function of i

        x = (a + b) * cos(t) - h * cos(i * (a + b) / b);
        y = (a + b) * sin(t) - h * sin(i * (a + b) / b);



        vertex(x, y);


    }
    endShape(CLOSE);

}

function drawFermat() {

    var x;
    var y;

    var a = map(mouseX, 0, width, 0, width);
    var b = a / 2;
    var h = height / 2;
    var ph = mouseX / 10;


    beginShape();
    for (var i = 0; i < nPoints; i++) {

        //defining angle variable for function

        var angle = map(i, 0, nPoints, 0, TWO_PI);


        x = (a - b) * sin(angle) - b * sin(angle * (a - b));
        y = (a - b) * cos(angle) - b * cos(angle * (a - b));

        vertex(x, y);


    }
    endShape(CLOSE);

}

In this project, I was able to use curve equations to generate highly complex and articulated line patterns that change with the location of the mouse. By using mapped numbers and for loops that iterate upon the functions the line patterns become layered and produce interesting effects as the overall patterns change. From there, I was able to use variables to change the color of the lines as the mouse position changes, and subsequently the background to match the line colors as they adapt. By using variables for many of the inputs, the results become highly varied and complex. 

Margot Gersing – Project 7 Curves

(click on shapes to activate)

This project I was inspired by some of the shapes shown as examples on the project description. I thought the round shapes were really cute and I could imagine them as a pattern. I made it so that each shape you could manipulate individually by clicking on them. This way there could be more options for what you could create based on the mouse.

>mgersing07

//Margot Gersing - Project 7 - mgersing@andrew.cmu.edu- section E

var oneX = 50; //for mouse press
var oneY = 50;
var act1 = false; //peach shape 'activation'

var twoX = 200; //for mouse press
var twoY = 350;
var act2 = false; //rusty orange shape 'activation'

var threeX = 400; //for mouse press
var threeY = 100;
var act3 = false; //pink shape 'activation'

var fourX = 500; //for mouse press
var fourY = 500;
var act4 = false; //gray shape 'activation'

var nPoints = 100;

function setup() {
    createCanvas(600,600);
    frameRate(10);

}

function draw(){
	background(230, 226, 222);
	noStroke();
	one();
	four();
	two();
	three();

	//filler shapes (static)
	fill(233, 154, 123);
	ellipse(50, 600, 400, 150);
	fill(233, 115, 88);
	ellipse(600, 125, 100, 150);
	fill(95, 44, 39);
	ellipse(150, 150, 25, 25);
	ellipse(175, 175, 20, 20);
	ellipse(135, 180, 25, 25);
	ellipse(185, 135, 25, 25);
	ellipse(155, 115, 20, 20);
	ellipse(500, 500, 20, 20);
	ellipse(490, 535, 25, 25);
	ellipse(600, 275, 25, 25);
	ellipse(575, 250, 25, 25);
	ellipse(560, 285, 20, 20);
	ellipse(60, 480, 25, 25);	

}

function one(){
	//peach shape
	var w1 = 200;
    var h1 = 200;

    //click to activate otherwise static
	if(act1){
		w1 = mouseX * .75;
		h1 = mouseY * .75;
	} else{
		w1 = 200;
		h1 = 200;
	}

	fill(240, 213, 189);
	ellipse(50, 50, w1, h1);
}

function two(){
	//epitrochoid
	var x;
    var y; 
    var a = 80.0;
    var b = a / 2.0;
    var h2 = constrain(100 / 8.0, 0, b);
    var ph2 = 100 / 50.0;

    //click to activate otherwise static
    if(act2){
		h2 = constrain(mouseX / 8.0, 0, b);;
		ph2 = mouseX / 50.0;
	} else{
		h2 = constrain(100 / 8.0, 0, b);
		h1 = 100 / 50.0;
	}
    fill(205, 100, 77);
    beginShape(); //drawing shape
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        
        x = (a + b) * cos(t) - h2 * cos(ph2 + t * (a + b) / b);
        y = (a + b) * sin(t) - h2 * sin(ph2 + t * (a + b) / b);
        vertex(x + 200, y + 350);
    }
    endShape(CLOSE);
}

function three(){
	//cranioid
	var x;
    var y;
    var r;
    var a = 40.0;
    var b = 10.0;
    var c = 100.0;
    var p = constrain((width/2), 0.0, 1.0);
    var q = constrain((height/2), 0.0, 1.0);

    //click to activate otherwise static
    if(act3){
    	var p = constrain((mouseX / width), 0.0, 1.0);
        var q = constrain((mouseY / height), 0.0, 1.0);
    } else{
    	var p = constrain((width/2), 0.0, 1.0);
        var q = constrain((height/2), 0.0, 1.0);
    } 
    fill(227, 187, 202);
    beginShape(); //drawing shape 
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        r =
            a * sin(t) +
            b * sqrt(1.0 - p * sq(cos(t))) +
            c * sqrt(1.0 - q * sq(cos(t)));
        
        x = r * cos(t);
        y = r * sin(t);
        vertex(x + 400, y + 100);
    }
    endShape(CLOSE);
}

function four(){
	//gray shape
	var w4 = 200;
    var h4 = 300;

    //click to activate otherwise static
	if(act4){
		w4 = mouseX;
		h4 = mouseY;
	} else{
		w4 = 200;
		h4 = 300;
	}

	fill(37, 45, 46);
	ellipse(475, 475, w4, h4);
}


function mousePressed(){

	//if clicked within in defined distance then activation state is... 
	   //changed from true to false so the mouseX and mouseY will now take over
	var d = dist(oneX, oneY, mouseX, mouseY);
	if(d < 200){
		act1 = !act1;
	}

	var d2 = dist(twoX, twoY, mouseX, mouseY);
	if(d2 < 100){
		act2 = !act2;
	}

	var d3 = dist(threeX, threeY, mouseX, mouseY);
	if(d3 < 100){
		act3 = !act3;
	}

	var d4 = dist(fourX, fourY, mouseX, mouseY);
	if(d4 < 100){
		act4 = !act4;
	}

}

Sarah Choi – Project 07 – Composition with Curves

project-07

//Sarah Choi 
//Section D
//sychoi@andrew.cmu.edu
//Project-07

var col;

function setup() {
    createCanvas(400, 400);
}

function draw() {
    background(0);

    //randomize color
    col = color(random(255), random(255), random(255));

    x = constrain(mouseX, 0, width);
    y = constrain(mouseY, 0, height);
    
    // draw the frame
    fill(255); 
    noStroke();
    text("The Butterfly", 20, 40);
    stroke(255);
    noFill(); 
    rect(0, 0, width-1, height-1); 
    
    // draw the curve, rotate on mouseX
    push();
    translate(width / 2, height / 2);
    rotate(map(mouseX, 0, width, 0, 1));
    drawButterfly();
    pop();
}

//--------------------------------------------------
function drawButterfly() {
    // Butterfly Curve:
    // http://mathworld.wolfram.com/ButterflyCurve.html
 
    //adding variability and movement
    var m = (map(x, 0, mouseY, 0, width)); 
    var m = (map(y, 0, mouseX, 0, height));

    stroke(255);
    fill(col);

    beginShape();
    for (var i = 0; i < 300; i++) {
        var t = map(i, 0, 300, 0, 2 * TWO_PI);
        
    //butterfly curve equations
        r = (exp(cos(t))) - (2 * cos(4 * t)) + (sin((1 / 12) * t));

        x = r * sin(t) * m
        y = r * cos(t) * m
        vertex(x, y)
    }
    endShape(CLOSE);
}

I chose a curve that could turn on an angle. Thinking of fully randomizing and creating something abstract on the basis of mathematics was my main goal for this project. Because we have been focusing and reflecting on computational art, I wanted to be able to portray this with my own work. It was interesting to play around with the variables as they made a big difference in how the curve was portrayed.

Below, I have shown three different aspects of the curve showing the beginning and how it manifests as it follows the x and y coordinates of the mouse. I wanted to show portray nature by showing the beginning of a butterfly as pure blackness. As one moves the mouse, the shapes get bigger with colors constantly changing showing the beauty butterflies bring into our world. As the mouse moves more across the screen, the butterfly gets bigger to depict what the human eye takes in as a butterfly flies closer to him or her.

Alec Albright – Project 07 – Curves

sketch

// Alec Albright
// aalbrigh@andrew.cmu.edu
// Section B
// Project 07

var nPoints = 100; // number of points used to draw curves

function setup(){
    createCanvas(480, 480);
    angleMode(RADIANS);
}

function draw(){
    background("lightpink");

    // center the shapes
    push();
    translate(width / 2, height / 2);

    // draw all the shapes
    drawHippopede();
    drawEpicycloid();
    drawHypotrochoid();

    pop();
}

// draws Hippopede
function drawHippopede() {
    var x; // x coordinate of vertex
    var y; // y coordinate of vertex
    var r; // polar coordinate
    var a = mouseX / 2 // main parameter of the curve
    var b = map(a, 0, 480, 100, 240); // circle radius
    var rotation = map(mouseY, 0, 480, 0, TWO_PI); // amount of rotation

    // thickness of line proportional to the circle radius
    strokeWeight(b / 5);
    stroke("white");
    noFill();

    // rotate shape
    push();
    rotate(rotation);

    // start drawing the shape, one point at a time
    beginShape();
    for(var i = 0; i < nPoints; i++){
        var t = map(i, 0, nPoints, 0, TWO_PI);
        
        // find r (polar equation)
        r = sqrt(4 * b * (a - b * sinSq(t)));

        // convert to x and y coordinates
        x = r * cos(t);
        y = r * sin(t);

        // draw a point at x, y
        vertex(x, y);
    }
    endShape();
    pop();
}

// draws hypotrochoid
function drawHypotrochoid() {
    var x; // x coordinate of vertex
    var y; // y coordinate of vertex
    var a = map(mouseX, 0, 480, 50, 150); // radius of the interior circle
    var b = 3; // radius of the petals
    var h = mouseX / 10; // distance from center of interior circle
    var red = map((mouseX + mouseY) / 2, 0, 480, 0, 255); // how much red
    var blue = map(mouseY, 0, 480, 0, 255); // how much blue
    var alpha = map(mouseX, 0, 480, 50, 255); // how opaque
    var rotation = map(mouseY, 100, 300, 0, TWO_PI); // amount of rotation

    strokeWeight(2)
    stroke("white");

    // control color and opacity with mouse location
    fill(red, 0, blue, alpha);

    // control rotation with mouseY
    push();
    rotate(rotation);

    // create the shape itself
    beginShape();
    for(var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);

        // use parametric euqations for hypotrochoid to find x and y
        x = (a - b) * cos(t) + h * cos((a - b) / b * t);
        y = (a - b) * sin(t) - h * sin((a - b) / b * t);

        // draw a point at x, y
        vertex(x, y)
    }
    endShape(CLOSE);
    pop();
}

// draws an epicycloid
function drawEpicycloid() {
    var x; // x coordinate of vertex
    var y; // y coordinate of vertex
    var a = map(mouseX, 0, 480, 50, 200); // radius of interior circle
    var b = map(mouseY, 0, 480, 10, 50); // radius of petals
    var blue = map((mouseX + mouseY) / 2, 0, 480, 0, 255); // how much blue
    var red = map(mouseY, 0, 480, 0, 255); // how much red
    var rotation = map(mouseY, 100, 300, 0, TWO_PI); // how muhc rotation

    // control color with mouse location
    strokeWeight(10)
    stroke(red, 0, blue);

    // control rotation with mouse location
    push();
    rotate(rotation);

    // start drawing shape
    beginShape();
    for(var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);

        // find coordinates using epicycloid parametric equations
        x = (a + b) * cos(t) - b * cos((a + b) / b * t);
        y = (a + b) * sin(t) - b * sin((a + b) / b * t);

        // draw a point at x, y
        vertex(x, y);
    }
    endShape();
    pop();
}

// defines sin^2 using trigonometric identities
function sinSq(x) {
    return((1 - cos(2 * x)) / 2);
}

In order to put together this project, I started with a simple curve, the hippopede, and began to implement increasingly more complex ones. Once I was able to draw the three curves (hippopede, hypotrochoid, and epicycloid), I started mapping various features of the curves to things like color, transparency, stroke weight, and rotation until I was satisfied with the results. Particularly, the color mapping was interesting to me because I utilized the average of the mouseX and mouseY coordinates in order to determine some aspects of color like the amount of red in the hypotrochoid and the amount of blue in the epicycloid. This allowed me to have more freedom to speculate interesting relationships that could be created using the coordinate system.

mouseX = 400, mouseY = 50
mouseX = 240, mouseY = 400
mouseX = 50, mouseY = 200
mouseX = 480, mouseY = 240

Alice Cai Project 7

sketch

//alcai@andrew.cmu.edu
//alice cai
//section E
//Project Week 7

//spinning speed
var speed = 0;

function setup() {
    createCanvas(500,500);
}

function draw() {
    frameRate(30);
    background('black');

    push();
    //draw at middle of canvas
    translate(width/2, height/2);
    //rotate speed, rotates on its own but also adjusted by mouse X
    rotate(speed + mouseX, 0, 200, 0, TWO_PI); 
    speed = speed + 1;
    //call droid draw functions
    epicycloid();
    astroid();
    epitrochoid();
    pop();

}


function epicycloid(){ 
    noFill();
    strokeWeight(2);
    stroke(mouseX, 100, 130,150);
    

    beginShape();
    //defining variables, size is corntroled by mouseX/mousY
    a = map(mouseX, 0, width, 50,300);
    b = map(mouseY, 0, width, 50,300);
    //forloop that repeats shape
    for (var t = 0; t < 40; t ++) {
    var x = (a / (a + 2 * b)) * cos(t) - b * cos(((a + b) / b) * t);
    var y = (a / (a + 2 * b)) * sin(t) - b * sin(((a + b) / b) * t);
    vertex(x ,y);
    endShape();

}
}

function epitrochoid (){
    noFill();
    strokeWeight(5);
    stroke(200,10,100, 5);

    beginShape();

    //forloop that repeats shape
    for (var i = 0; i < 100; i ++) { 

    //defining variables, size is corntroled by mouseX/mousY
    a = map(mouseX, 0, width, 50,300);
    b = map(mouseX, 0, width, 50,300);
    h = map(mouseX, 0, width, 50,200);  

    x = (a + b) * cos(i/2) - (h * cos((a + b / b) * i));
    y= (a + b) * sin(i/2) - (h * sin((a + b / b) * i));
    vertex(x, y);
    endShape();
    }
}



function astroid(){ 
    noFill();
    strokeWeight(5);
    stroke(130, 100, 150,150);

    

    beginShape();

    //forloop that repeats shape
    for (var t = 0; t < 20; t ++) {
        
    //defining variables, size is corntroled by mouseX/mousY
    z = map(height - mouseY, 0, width, 50,200);
    var x = z * cos(t)^ 3 ;
    var y = z * sin (t)^ 3 ;
    vertex(x ,y);
    endShape();

    }

}

This project seemed really daunting because all the shapes looked complex and there was a lot going on on the screen, especially those with mouse interaction. Turns out, it’s not as complex as it seems. Although the equations may seem complex, they are also given to us. After that, it’s just about defining the variables in the equation and calling a for loop to draw a pattern with the shape! I used a map function to control the size of the shape with mouseX and mouseY. I also changed the opacity of the line strokes for a more transparent and three-dimensional looks.

TWO SHAPES
THREE SHAPES with varying opacity
A better capture of the visual effect of lower opacity