Category: Section E

katieche-project-07

katieche-07

/*
katie chen
katieche@andrew.cmu.edu
project 07
section E
*/

function setup() {
    createCanvas(480, 480);
}

function draw() {
    background(255, 210, 190);
    var mx = constrain(mouseX, 60, 450);

push();
beginShape();
    // points 
    var n1 = 400;
    // big circle radius
    var a1 = 100;
    // small circle radius
    var b1 = map(mx, 0, width, 0, 10);
    // distance from center of the interior circle to P (what draws the line)
    var h1 = map(mx, 0, width, 0, 300);

    noFill();
    stroke(255, 222, 221);
    strokeWeight (0.2);
    translate(width/2, height/2); //center the object
    for(var i = 0; i < n1; i++) {
        var t = map(i, 0, n1, 0, TWO_PI); 
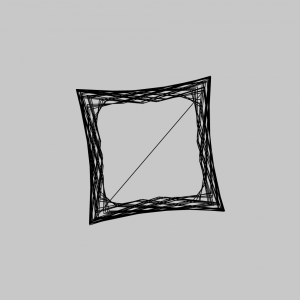
        var x1 = (a1-b1)*cos(t) + h1*cos(t*(a1-b1)/b1)
        var y1 = (a1-b1)*sin(t) + h1*sin(t*(a1-b1)/b1)
        vertex(x1, y1);
endShape();
    }
pop();

push();
beginShape();
    // points
    var n = 400;
    // big circle radius
    var a = map(mouseY, 0, height, 0, 200);
    // small circle radius
    var b = 10;
    // distance from center of the interior circle to P (what draws the line)
    var h = map(mouseX, 0, width, 0, 200);
    noFill();
    stroke(255, 231, 226);
    strokeWeight (0.2);
    translate(width/2, height/2); //center the object
    for(var i = 0; i < n; i++) {
        var t = map(i, 0, n, 0, TWO_PI); 
        var x = (a-b)*cos(t) + h*cos(t*(a-b)/b)
        var y = (a-b)*sin(t) + h*sin(t*(a-b)/b)
        vertex(x, y);
endShape();
    }

pop();


}

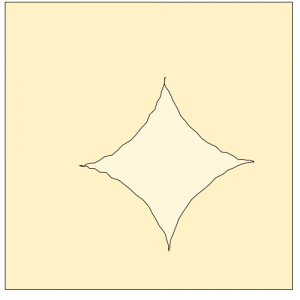
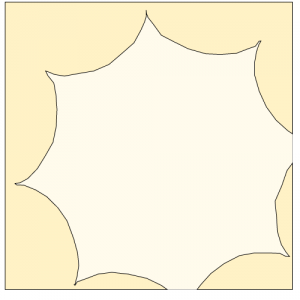
I wanted to create 2 shapes, one that has less points and shows more of the shape being drawn, and one that’s super complicated. The pinker shape is more complicated so I constrained it before it jumbles into a solid donut shape.

The white line shape is what I like more since if you place your mouse near the center-left hand side of the canvas and move your mouse from the top to the bottom of the canvas, you can kind of see the spirograph being drawn. Moving your mouse from left to right makes the swirls bigger.

Sheenu-Looking Outwards-07

http://infosthetics.com/archives/2014/03/browser_plugin_maps_browser_history_as_a_favicon_tapestry.html

This is a project created on accident by CMU student Shan Huang in 2014. It’s a Google chrome plugin that looks through a user’s history and collects all the favicons of all the websites visited. It then organizes all the favicons and arranges them into a large mural based on oldest link to newest. Each image is still functional, so when clicked it will redirect you to the original website. What I really like about this project is how it transforms everyday online browsing into an art form. It also shows us the overwhelming amount of times people use the internet and go on a website in a day or just an hour in just one image. It’s truly a beautiful but also very reflective and realistic piece.

dayoungl Looking Outwards – 07

Map of seoul represented through patterns
Map of Venezia represented through texts and pictograms of tourist attractions and architectures
Map of Amazon River, Brazil represented in terms of the degree of deforestation

Map of Ozeros (lakes in Russian)

Map is one of the most notable use of information visualization in a way that it is a combination of information based on carefully formulated intention and utility. For creating a map, designers need to take multiple things into consideration: the quality of aesthetics, readability, and most importantly, delivery of information. For this week’s looking outwards, I looked into graphic maps created by Amoeba Group based in Seoul, Korea. Amoeba Group focuses on data visualization, specializing in transferring the data onto a two-dimensional map.

From an interview of CEO of Amoeba Group I found on the web, he states that they first refer to google Earth and Open Street Maps to figure out the the tiniest alleys and streets names when studying the geographical data. Then, they move on to learn about the traditional map-making process, understanding the logistics and the characteristics of maps. Once that’s finished, they move on to understanding the specific geographical and cultural significance of the region of the map.

I found this map project particularly interesting because; first, I was very drawn to the graphic quality of the project; second, map is an area of data visualization that I seemed to have overlooked.

jwchou-LookingOutwards-07

Project: American Panorama by Stamen Inc.

A map by Stamen showing foreign-born populations in the USA using data. Each country is shown proportionally by size.

Stamen is a company that specializes in very unique and data-centered visualizations. Many of their projects are based on geography/mapping.

For one of their projects in collaboration with Mellon Foundation, Stamen created a suite of software tools that generate maps! They used their software to make maps that portrayed a diverse set of data about America, such as physical objects (canals and trails) and statistics such as foreign-born populations in America. The creators’ artistic sensibilities are portrayed in the different aesthetic choices of the maps, such as color, layout, type choice, etc… (graphic design).

I really admire how they made the software accessible on GitHub for anyone to use/explore, which shows that they realize how data visualization can be a powerful tool for education.

American Canals

These maps were a collaborative effort with the Digital Scholarship Lab. They analyzed and compiled many data sets, and Stamen used their software to visualize it.

alchan-Project 07-curves

curves

// attributes of shape
var points;
var angle;

function setup() {
  createCanvas(480, 480);
  angleMode(DEGREES);
  frameRate(30);
}

function draw() {
  background(200);
  // set attributes to change with mouse position
  points = map(mouseX, 0, width, 0, 300);
  angle = map((mouseX + mouseY / 2), 0, width, 0, 360);
  // draw "main" curve
  stroke(209, 122, 110);
  drawCurve(width/2, height/2);

  // draw "background" curves, setting each to a random color
  // and a randomized position
  stroke(random(200, 255), random(200, 255), random(200, 255));
  drawCurve(width/2 + random(-10, 10), height/2 + random(-10, 10));
  stroke(random(200, 255), random(200, 255), random(200, 255));
  drawCurve(width/2 + random(-20, 20), height/2 + random(-20, 20));
  stroke(random(200, 255), random(200, 255), random(200, 255));
  drawCurve(width/2 + random(-30, 30), height/2 + random(-30, 30));
  stroke(random(200, 255), random(200, 255), random(200, 255));
  drawCurve(width/2 + random(-40, 40), height/2 + random(-40, 40));
}

function drawCurve(posX, posY) {
  var x;
  var y;
  //var a = 400;
  var b = map(mouseY, 0, 480, 20, 80);

  strokeWeight(1);
  noFill();

  push();
  translate(posX, posY);
  rotate(angle);
  // astroid curve (http://mathworld.wolfram.com/Astroid.html)t
  beginShape();
  for (var i = 0; i < points; i++) {
    x = 3 * b * cos(i) + b * cos(3* i);
    y = 3 * b * sin(i) - b * sin(3 * i);
    vertex(x + random(0,2), y + random(0,2));
  }
  endShape(CLOSE);
  pop();
}

Since I was a little overwhelmed with the idea of creating a project based on mathematical curves, I decided to approach the project by “sketching” in the browser and figuring out how the code/ curve would render as I modified different variables. I chose an astroid for my curve. I also hadn’t originally set the angle mode of the drawing to degrees, and ended up with a spirograph-like drawing at first which was visually interesting, but not quite what I was going for.

Once I had figured out how to make the curve actually a curve, I added in variables to make the size, number of points drawn, and rotation of the curve interactive. I also added elements of randomization to try to achieve a flickering/ glitching effect to add more interest.

mecha-project07-curves

sketch

//maddy cha
//section e
//mecha@andrew.cmu.edu

var nPoints = 100;

function setup() {
    createCanvas(480,480);
}

function draw() {
    //background g value is increased with mouseX
    background(255,constrain(map(mouseX,0,width,0,255),210,240),200);   
    frame();
    //location of curve depends on mouse (but is constrained 60 pixels around center in x and y directions)
    translate(constrain(mouseX,width/2-30,width/2+30),constrain(mouseY,height/2-30,height/2+30));
    hypocycloid();
}

//draws outside black rectangle
function frame(){
    noFill();
    stroke(0);
    rect(0,0,width-1,height-1);
}

function hypocycloid(){
    var x;
    var y;
    var r;
    var a = map(mouseX,0,width,0,150);
    //increases amount of points on hypocycloid
    //makes it so that points are increasing by whole numbers
    var b = nf(map(mouseX,0,width,0,6),2,0);

    push();
    //rotates based on mouseX location
    rotate(mouseX);
    //opacity of shape is dependant on mouseX
    fill(256,256,256,map(mouseX,0,width,0,100));
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        
        x = (a/b)*((b-1)*cos(t)-cos((b-1)*t))
        y = (a/b)*((b-1)*sin(t)+sin((b-1)*t));
        //draws points at x and y values (with some randomness)
        //nPoints dictates how many points are drawn between lines
        vertex(x+random(-2,2), y+random(-2,2));
    }
    endShape(CLOSE);
    pop();
}

For this project, I started with creating a deltoid by implementing the formula into my code. Once I was able to understand how to do this, I wanted to expand my scope by looking at the overarching hypocycloid. I decided that I wanted my mouseX and mouseY interactions to increase the amount of cusps that would appear on my shape. In order to do this, I had to alter my original deltoid formula to take in a greater amount of variables.

Once I figured that out, I implemented more ways in which the user could interact with my code using their mouse. I relied on the constrain() and map() functions in order to make sure the shape stayed in the canvas. While mouseY was used to change the location of my shape, mouseX dictated the amount of cusps, the color of the background color, the size, fill opacity, and the rotation of the hypocycloid. Additionally I experimented with adding randomness so that my project would be more visually entertaining.

mecha-lookingoutwards-07

Touching Air

For this week, I decided to look into the work of Stefanie Posavec, specifically her explorations with wearable data visualizations. Collaborating with information researcher Miriam Quick, Posavec created this piece titled Touching Air in 2014. The two collected data regarding large particulate (PM10) levels. Each necklace they created in this series was meant to visualize a week’s worth of data, with the size and shape of each piece representative of the amount of particulates in the air. The large, spiky piece in the image above represents the fact that there are a dangerous amount of particulates in the air–making the piece harmful to touch.

Posavec wrote that her decision to visualize this data using a necklace had to do with how these specific particulate levels are harmful to one’s heart and lungs. When I imagine data visualizations, my mind immediately thinks of graphs and other two-dimensional ways of visualizing data. Because of how this went against the norm of what I consider to be data visualizations, I felt that it was an interesting piece to dissect. I was inspired with how the communication of the data was representational of the issues that the subject brings about.

yoonyouk-lookingoutwards-07

This week’s looking outwards I focused on the work of Periscope, a company that focuses on data collection and visualization. Their goal is to send a message to their audiences and engage the public. Their visualization of data is very unique and provides a creative outlook data trends. For example, in data collection titled, “Most Negative Inaugural Speech in Decades.” I thought this data collection was unique in many ways – one being that they made quantitative data of facial expressions. Microsoft API was used to detect facial expressions while the presidents were speaking. A unique algorithm must have been crafted in order to detect facial expression and then determine whether it is positive or negative. They then combined all of the emotions into an arc like formation, creating a feather-like graph.

Above is the graph for President Trump’s inaugural speech. The graph shows a lot of negative emotions arising.

Rather than taking a typical approach of data visualization, such as a bar graph of a pie chart, the designers utilized a unique shape that still represented the appropriate data. When clicking on the individual strokes of the feather, users were able to detect the specific feelings felt during the speech.

 

alchan-Looking Outwards 07

(an example of the July 12, 2013 “Manhattanhenge”)

NYCHenge, created by the Carto team in 2013, is a project that visualizes how the sun aligns with the streets of New York City, inspired by the two times a year the sun lines up with the midtown grid of streets (“Manhattanhenge”). Sun-alignment is indicated by orange or red colors; the more red the color gets the more in-line the sun will be with that particular street. Users can explore the entire city of New York (not just Manhattan) across the entire year to find other, mini-henges or just figure out when the sun will shine in their faces as they’re driving down certain streets. It’s created with Open Street Maps, CartoDB tools, and the SunCalc javascript library to figure out the sun position.

I was drawn to this project because of its interesting focus, and the way it’s both interactive and relatively easy to understand. One downside to the simplicity of the map is that non-New-Yorkers will probably have trouble identifying the unlabeled streets, but the general gist of the project is still obvious.

LookingOutwards06-jooheek

Marius Watz: Random Numbers

Link: https://creators.vice.com/en_us/article/vvzxkb/random-numbers-screen-printed-generative-art-nyc-event

Marius Watz “Arcs04-01” from the series Random Numbers Multiples

In the project, Random Numbers, Marius Wats, a generative artist, collaborates with Jer Thorp to create a series of visualizations that demonstrates data of random numbers. They described that their project is about “pseudo-random compositions of radial shapes, subtly distorted by a 3D surface that lends the image a strong focal point and sense of movement.”

Marius Watz “Arc04-00” from the series Random Numbers Multiples

I think that the randomness of this artwork really adds to the aesthetic of the piece. The artist combines two factors that are usually not juxtaposed together: randomness and data. Data is something that is really not random but by adding randomness to it, the artist demonstrates an aesthetic for the visualization.