//Elise Chapman
//ejchapma
//ejchapma@andrew.cmu.edu
//Section D
var nPoints = 100; //number of points along the curve
var noiseParam=5;
var noiseStep=0.1;
var petalNum=1; //number of petals on curve
var x; //for points along curve
var y; //for points along curve
function setup() {
createCanvas(480,480);
frameRate(10);
}
function draw() {
background(0);
//draws the epitrochoid curve
//Cartesian Parametric Form [x=f(t), y=g(t)]
push();
translate(width/2, height/2);
var a = 90;
var b = a/petalNum;
var h = constrain(mouseY / 8.0, 0, b);
var ph = mouseX / 50.0;
fill(mouseY,0,mouseX);
noStroke();
beginShape();
for (var i = 0; i<nPoints+1; i++) {
var t = map(i, 0, nPoints, 0, TWO_PI); //theta mapped through radians
//Cartesian Parametric Form [x=f(t), y=g(t)]
x = (a + b) * cos(t) - h * cos(ph + t * (a + b) / b);
y = (a + b) * sin(t) - h * sin(ph + t * (a + b) / b);
var nX = noise(noiseParam); //noise for x values
var nY = noise(noiseParam); //noise for y values
nX=map(mouseX,0,width,0,30);
nY=map(mouseY,0,height,0,30);
vertex(x+random(-nX,nX),y+random(-nY,nY));
}
endShape(CLOSE)
pop();
}
//click to increase number of petals on the curve
function mousePressed() {
petalNum+=1;
if (petalNum==6) {
petalNum=1;
}
}
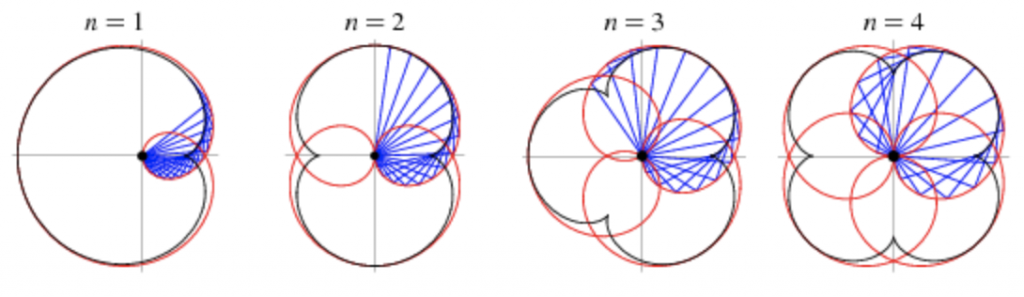
To begin, I liked the movement that was created by Tom’s example epitrochoid curve, so I went to the link he provided on Mathworld and read about the curve. I understood that I could make the petals interactive by adding a click into the program and changing the value of b in the curve equation. So at this point, my program allowed from 1 to 5 petals depending where in the click cycle the user is.

Then, I thought back to one of the previous labs, where we would draw circles with variable red and blue fill values, which I really enjoyed aesthetically. So, I made the blue value variable dependent upon the mouseX value and the red value variable upon the mouse Y value.


Finally, I really enjoyed the jittery star from the class example from our lecture on Randomness and Noise, so I decided I wanted to add noise. Because the curve is drawn with a series of points, I added noise randomness to each of the points, affecting both the x scale and the Y scale. Overall, I enjoy how the final project came out. I think it would be a cool addition to the header of a website, especially if I’m able to make the background transparent.

![[OLD SEMESTER] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2023/09/stop-banner.png)