Category: Uncategorized

sketch

//Steph Chun
//15-104 section #A
//heeseoc@andrew.cmu.edu
//Project-07

var a = 30;
var b = 10;
var t = 500;
var h = 80;

function setup() {
    createCanvas(400, 400);
    frameRate(10);
}

function draw() {
	background(0);
	stroke(255);

	push();
	translate(width/2, height/2);
	beginShape();

	//lines//
	for (var i = 0; i < 50; i++) {
		var Xcoord = ((a-b)*cos(i))+(h*cos(((a-b)/b)*i));
		var Ycoord = ((a-b)*sin(i))+(h*sin(((a-b)/b)*i));
		var Xcoord2 = ((a-b)*cos(i-t))+(h*cos(((a-b)/b)*(i-t)));
		var Ycoord2 = ((a-b)*sin(i-t))+(h*sin(((a-b)/b)*(i-t)));
		b = mouseX + 650;
		line(Xcoord + random(-3, 3), Ycoord+ random(-3, 3), Xcoord2+ random(-3, 3), Ycoord2+ random(-3, 3));
    	
    	//bubbles//
		push();
		rotate(i);
    	ellipse (i + random(-3, 3), Ycoord, 2, 2);
    	ellipse (i + random(-3, 3), Ycoord2, 4, 4);
    	ellipse (Xcoord, i + random(-3, 3), 2, 2);
    	ellipse (Xcoord2, i + random(-3, 3), 4, 4);
    	pop();
    }
    endShape(CLOSE);
    pop();
    
    //bigger circle//
    push();
    translate(width/2, height/2);
    beginShape();
    for (var i = 0; i < 20; i++) {
    	fill(255, 50);
        var theta = map(i, 0, 20, 0, TWO_PI);
        var x = mouseX * 0.25 + 60;
        var px = x * cos(theta);
        var py = x * sin(theta);
        vertex(px + random(-3, 3), py + random(-3, 3));
    }
    endShape(CLOSE);
    pop();

    //smaller circle//
    push();
    translate(width/2, height/2);
    beginShape();
    for (var i = 0; i < 20; i++) {
    	fill(0);
        var theta = map(i, 0, 20, 0, TWO_PI);
        var x = mouseX * 0.25 + 20;
        var px = x * cos(theta);
        var py = x * sin(theta);
        vertex(px + random(-3, 3), py + random(-3, 3));
    }
    endShape(CLOSE);
    pop();

}

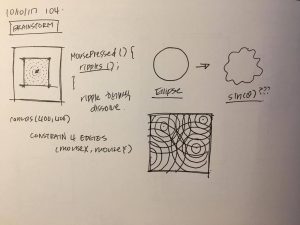
For this project, I started off with browsing mathworld website and finding the curve that we would want to use. I chose hypotrochoid. Then, I tried to generate that curve through coding, and what I found out was at some point, the lines that I made through the equation I chose made an eye-shaped form at some point, so I restricted the mouse movement to have it start from the shape and added wiggly circles in the middle of those lines. I added the wiggly bubbles in the back because it felt like it needed some more elements to it to have some sort of a visual balance. I kept all the colors white, because I did not want it to be way to literal in communicating my “zooming into an eye” idea. Below is the screenshot of the shape I got inspired from.

sketch

//Helen Wu
//Section A
//hdw@andrew.cmu.edu
//Project 7

function setup() {
    createCanvas(480,480);
    background(255, 71, 123)
}


function draw() {
  push();

  //this is to call the centers of which the sextic functions will be called from
  translate(width/2, height/2);
  beginShape();
  for(var i = 0; i < 25; i++){
    //25 sets the direction of which the curves draw
      var t = map(i,0,100,0,360);
      //t = angle
      var a = map(mouseY, 0, 480, -5, 5);
      //a = control the curvature of the loops
      var x = 4*a*(Math.pow(cos((1/3)*t),3))*cos(t);
      var y = 4*a*(Math.pow(cos((1/3)*t),3))*sin(t);
      //centerX and centerY = center of smaller curves
      var centerX = 10*x
      var centerY = 10*y
  }
  endShape(CLOSE);
  pop();


//drawing below sextics on points along above sextic
  cayleysSextic(centerX, centerY);
  }

function cayleysSextic(centerX,centerY) {
  push();
  //placement of sextics along center
  translate(width/2+centerX,height/2+centerY);
  beginShape();
  for(var i = 0; i < 50; i++){
      //t = angle
      var t = map(i,0,100,0,360);
      //a = control the curvature of the loops
      var a = map(mouseX, 0, 400, -10,10);
      var x = 4*a*(Math.pow(cos((1/3)*t),3))*cos(t);
      var y = 4*a*(Math.pow(cos((1/3)*t),3))*sin(t);
      //center of smaller loop's smaller curves
      noStroke()
      fill(255,255,255,30);
      ellipse(x*3,y*3,1,1);
      //drawing ellipses along the curve
  }
  endShape(CLOSE);
  pop();
}

This project was based on Cayley’s Sextic, which coincidentally looks like a butt. 👀👀

I mapped Cayley’s Sextic along another Cayley’s Sextic, just to see how it would look. I kind of like how cute the final product turned out to be. The centers of one are along the next, both mapped to the mouse position on the canvas.

project04.js

function setup() {
    createCanvas(480, 480);
    angleMode(DEGREES);
    frameRate(50); //delayed feedback so lines appear to draw themselves and disappear
}

function draw() {

//making the colour of the background dependent on the cursor position
    background(mouseX/7.55, mouseY/20, mouseX/15, mouseY/20); 
    //the trasnparency of the backgroud is also dependent on the cursor position

//changing the position of the start point of the curves. 
    translate (width/3,height/2);
    noFill();

//creating the for loop variables for which the angles will change
    for (var i = 0; i < 361; i++){

        //maping the angles so they only go between 0 and 360 
        var t = map(i, 0, 360, 1, 500); 
        
        //making the colours only range 0 and 255 no matter cursor position
        var r = map(mouseX, 0, 1000, 250, 255); 
        var g = map(mouseX, 0, 1000, 120, 130);
        var b = map(mouseX, 0, 1000, 70, 80);

        //making the variables for the points' scaling
        var scale1 = 0.0005;  
        var scale2 = 0.5;
        var scale3 = 0.001;
        var scale4 = 0.4;

        //creating the curves of the graphs that the for loop is going to be used with
        var x1 = -sin(t)+cos(t);
        var y1 = cos(t);
        var x2 = cos(t) + 0.5;
        var y2 = sin(t);

        //creating the stroke colour and varying it according to the cursor position and the for loop
        stroke(r, g, t*(mouseX/800));
        strokeWeight(random(0.01, 0.05));

        line(x1*t*mouseX*scale1, y1*t*scale2, x2*t*scale2, y2*t*mouseY*scale1);
        line(x1*t*scale4, y2*t*mouseX*scale3, x2*t*mouseY*scale1, y2*t*scale4);

        push();
        //rotating the same two curves to create the rose like shape.
        rotate(90);
        
        line(x1*t*mouseX*scale1, y1*t*scale2, x2*t*scale2, y2*t*mouseY*scale1);
        line(x1*t*scale4, y2*t*mouseX*scale3, x2*t*mouseY*scale1, y2*t*scale4);
        
        pop();

    }
    
}

For this assignment I was inspired by a rose bud blooming and I was trying to figure out how to find an abstract way to represent it. I did this by changing the colours and have a frame rate that was slow enough for the lines to look like they were emerging from each other.

I experimented with cosine and sine curves and looked at what would happen if i multiplied, subtracted, added, and divided them from each other. I ended up with the above version because i felt that it represented the idea of the flower blooming the best.