// Joshua Brown
// Jdbrown@andrew.cmu.edu
// Project 7: Curves
// Section C
function setup () {
createCanvas (480, 480);
background (0);
}
function mousePressed () {
background (0);
}
function draw () {
stroke (255);
strokeWeight (2.5);
// defining variables for drawing line-heavy shapes;
// linking x variables with the mouseX parameter;
var x1 = mouseX;
var y1 = 40;
var x2 = mouseX;
var y2 = 440;
var xMid = width / 2;
var yMid = height / 2;
// drawing the spikey, Masonic symbol thing;
stroke (mouseX / 2 + 20, mouseX / 2, mouseY / 3);
line (x1, yMid, x2, yMid);
line (xMid, yMid / 4 - 30, xMid, yMid - 40);
line (xMid, yMid - 40, xMid - 180, yMid + 180);
line (xMid, yMid - 40, xMid + 180, yMid + 180);
line (xMid, yMid - 210, xMid + 180, yMid + 180);
line (xMid, yMid - 210, xMid - 180, yMid + 180);
line (x1, yMid, xMid, yMid - 150);
line (x2, yMid, xMid, yMid - 150);
line (x1, yMid, xMid, yMid - 80);
line (-x2 + 480, yMid, xMid, yMid - 80);
// drawing the inverse (upside-down version);
stroke (mouseY / 2, 0, mouseX / 3);
line (x1, yMid, x2, yMid);
line (xMid, yMid / 4 - 30, xMid, yMid + 40);
line (xMid, yMid + 40, xMid + 180, yMid - 180);
line (xMid, yMid + 40, xMid - 180, yMid - 180);
line (xMid, yMid + 210, xMid - 180, yMid - 180);
line (xMid, yMid + 210, xMid + 180, yMid - 180);
line (-x1 + 480, yMid, xMid, yMid + 150);
line (-x2 + 480, yMid, xMid, yMid + 150);
line (-x1 + 480, yMid, xMid, yMid + 80);
line (x2, yMid, xMid, yMid + 80);
fill (255);
ellipse (width/2, height/2, 30, 30);
// drawing the circles which comprise the central diamond shape;
push();
translate (width/2, height/2);
rotate (radians (mouseX));
fill (255, 25);
ellipse (-240, -240, 600, 600);
ellipse (-240, height - 240, 600, -600);
ellipse (width - 240, -240, 600, 600);
ellipse (width - 240, height - 240, 600, 600);
pop ();
// drawing circles on the fringes, to increase dimensionality;
push ();
translate (width/2, height/2);
rotate (radians (mouseY));
fill (0, 25);
ellipse (-240, -240, 300, 300);
ellipse (-240, height - 240, 300, -300);
ellipse (width - 240, -240, 300, 300);
ellipse (width - 240, height - 240, 300, 300);
pop ();
// drawing smaller fringe circles to increase trippiness;
push ();
translate (width/2, height/2);
rotate (radians (mouseX));
fill (0, 25);
ellipse (-240, -240, 150, 150);
ellipse (-240, height - 240, 150, -150);
ellipse (width - 240, -240, 150, 150);
ellipse (width - 240, height - 240, 150, 150);
pop ();
// small white circles! Why not!
push ();
translate (width/2, height/2);
rotate (radians (mouseX));
fill (255);
ellipse (-240, -240, 80, 80);
ellipse (-240, height - 240, 80, -80);
ellipse (width - 240, -240, 80, 80);
ellipse (width - 240, height - 240, 80, 80);
pop ();
}
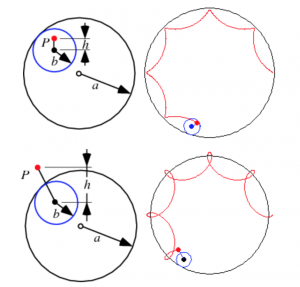
I was interested in the petal-ish curve shapes, since I didn’t quite understand how to translate a lot of the more complicated algebraic maths into code.
![[OLD FALL 2017] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)